Matrix Logarithm

The natural logarithm is the inverse operation of the exponential. The following equation defines the natural logarithm of a matrix A: e^B = A, where matrix B is the natural logarithm of matrix A. A matrix has a logarithm if and only if its inverse matrix exists. For a real matrix A, its logarithm matrix B can be complex, and the conjugate of matrix B is also the natural logarithm of A.

To obtain the logarithm of a diagonal matrix, you can calculate the logarithm of each diagonal element of the matrix. For example, if

then

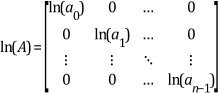
Thus, a common method of calculating the logarithm of a matrix is first to diagonalize the matrix and then to calculate the logarithm of each diagonal element of the new matrix. For example, consider the following:

• λ is a diagonal matrix whose diagonal elements are the eigenvalues of matrix A
• λ = V^-1AV, where V is the matrix composed of the eigenvectors of matrix A

If the previous two requirements are true, you can use the following equation to calculate the logarithm of A: ln(A) = V(lnλ)V^-1.

If you cannot diagonalize a matrix, you can use other methods, such as the Jordan Canonical Form or Taylor series expansion, to calculate the logarithm of the matrix.

The matrix logarithm satisfies the following properties:

• ln(I) = 0, where 0 is a zero matrix whose elements are zeros
• If ln(X)*ln(Y) = ln(Y)*ln(X), then ln(XY) = ln(X)+ln(Y)
• If Y is invertible, then ln(YXY^-1) = Yln(X)Y^-1
• ln(X*) = (ln(X))*, where X* is the transpose of the real matrix X, or the conjugate transpose of the complex matrix X