Basic Matrix Operations

Two matrices, A and B, are equal if they have the same number of rows and columns and their corresponding elements all are equal. Multiplication of a matrix A by a scalar α is equal to multiplication of all its elements by the scalar. That is,

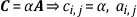
For example,

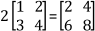
Two (or more) matrices can be added or subtracted only if they have the same number of rows and columns. If both matrices A and B have m rows and n columns, their sum C is an m × n matrix defined as C = A ± B, where c_i,j = a_i,j ± b_i,j. For example,

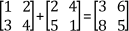
For multiplication of two matrices, the number of columns of the first matrix must be equal to the number of rows of the second matrix. If matrix A has m rows and n columns and matrix B has n rows and p columns, their product C is an m × p matrix defined as C = AB, where

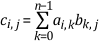
For example,

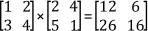
So you multiply the elements of the first row of A by the corresponding elements of the first column of B and add all the results to get the elements in the first row and first column of C. Similarly, to calculate the element in the ith row and the jth column of C, multiply the elements in the ith row of A by the corresponding elements in the jth column of C, and then add them all. This is shown pictorially in the following figure.

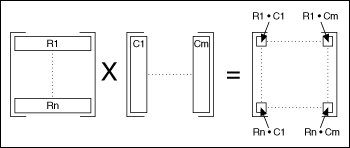
Matrix multiplication, in general, is not commutative, that is, AB ≠ BA. Also, multiplication of a matrix by an identity matrix results in the original matrix.