Matrix Exponential

The following equation defines the exponential of a matrix:

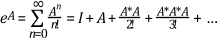
where I is the identity matrix.

To obtain the exponential of a diagonal matrix, you can calculate the exponential of each diagonal element of the matrix. For example, if

then

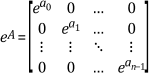
Thus, a common method of calculating the exponential of a matrix is first to diagonalize the matrix and then to calculate the exponential of each diagonal element of the new matrix. For example, consider the following:

• λ is a diagonal matrix whose diagonal elements are the eigenvalues of matrix A
• λ equals V^-1AV, where V is the matrix composed of the eigenvectors of matrix A

If the previous two requirements are true, you can use the following equation to calculate the exponential of A:

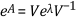
If you cannot diagonalize a matrix, you can use the Pade approximation method to obtain the exponential of the matrix. Because the derivatives of e^x are all ones at the zero point, you easily can calculate the derivatives you need for the Pade approximation method.

The exponential of a matrix satisfies the following properties:

• e⁰ = I, where 0 is a zero matrix whose elements are zeros
• e^Xe^-X = I
• If XY = YX, then e^{X + Y} = e^X e^Y
• For any matrix X, e^X is invertible and (e^X)^-1 = e^-X
• If Y is invertible, then exp(YXY^-1) = Yexp(X)Y^-1
• exp(X*) = (exp(X))*, where X* is the transpose of the real matrix X, or the conjugate transpose of the complex matrix X.