One of the most important attributes of a matrix is its determinant. In the simplest case, the determinant of a 2 × 2 matrix
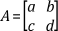
is given by ad - bc. The determinant of a square matrix is formed by taking the determinant of its elements. For example, if
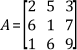
then the determinant of A, denoted by |A|, is
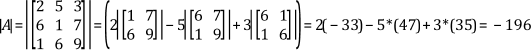
The determinant of a diagonal matrix, an upper triangular matrix, or a lower triangular matrix is the product of its diagonal elements.
The determinant tells many important properties of the matrix. For example, if the determinant of the matrix is zero, the matrix is singular. In other words, the previous matrix with nonzero determinant is nonsingular.
The following equation also is true for the determinant of a matrix: |AB|=|A| |B|.
The following list describes the three types of elementary operations and their effects on the determinant:
- The first type of elementary operation is to interchange two rows or two columns of a matrix. This operation changes the sign of the determinant of the matrix.
- The second type of elementary operation is to multiply a row or column of a matrix by a nonzero scalar. This operation multiplies the determinant of the matrix by the scalar.
- The third type of elementary operation is to add one row of a matrix multiplied by a scalar to another row or to add one column multiplied by a scalar to another column. This operation does not change the determinant of the matrix.