In matrix-vector notation, a system of linear equations has the form Ax = b, where A is an n � n matrix and b is a given n-vector. The aim is to determine x, the unknown solution n-vector. Whether matrix A is singular or nonsingular determines if such a solution exists and if it is unique.
A matrix is singular if it has any one of the following equivalent properties:
- The inverse of the matrix does not exist.
- The determinant of the matrix is zero.
- The rows or columns of A are linearly dependent.
- Az = 0 for some vector z ≠ 0.
Otherwise, the matrix is nonsingular. If the matrix is nonsingular, its inverse A-1 exists, and the system Ax = b has a unique solution, x = A-1b, regardless of the value for b.
On the other hand, if the matrix is singular, the number of solutions is determined by the right-hand-side vector b. If A is singular and Ax = b, A(x + αz) = b for any scalar α, where the vector z is as in the previous definition. Thus, if a singular system has a solution, the solution cannot be unique.
Explicitly computing the inverse of a matrix is prone to numerical inaccuracies. Therefore, you should not solve a linear system of equations by multiplying the inverse of the matrix A by the known right-hand-side vector. The general strategy to solve such a system of equations is to transform the original system into one whose solution is the same as that of the original system but is easier to compute. One way to do so is to use the Gaussian Elimination technique. The Gaussian Elimination technique has three basic steps. First, express the matrix A as a product
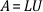
where L is a unit lower triangular matrix and U is an upper triangular matrix. Such a factorization is LU factorization. Given this, the linear system Ax = b can be expressed as LUx = b. Such a system then can be solved by first solving the lower triangular system Ly = b for y by forward-substitution. This is the second step in the Gaussian Elimination technique. For example, if
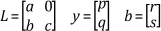
then
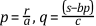
The first element of y can be determined easily due to the lower triangular nature of the matrix L. Then you can use this value to compute the remaining elements of the unknown vector sequentially�hence the name forward-substitution. The final step involves solving the upper triangular system Ux = y by back-substitution. For example, if
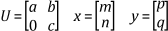
then
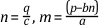
In this case, this last element of x can be determined easily and then used to determine the other elements sequentially�hence the name back-substitution. Because a non-square matrix is necessarily singular, the system of equations must have either no solution or a non-unique solution. In such a situation, you usually find a unique solution x that satisfies the linear system in an approximate sense.
It is important to identify the input matrix properly, as it helps avoid unnecessary computations, which in turn helps to minimize numerical inaccuracies. The four possible matrix types are general matrices, positive definite matrices, and lower and upper triangular matrices. A real matrix A is positive definite only if it is symmetric, and the quadratic form xTAx is positive for any nonzero vectors x.