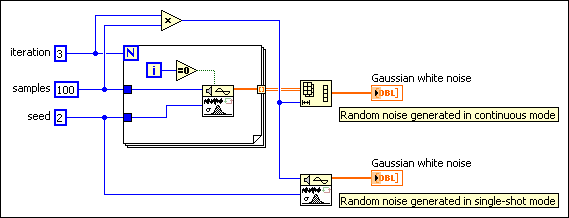
Gaussian White Noise VI
Owning Palette: Signal Generation VIs
Requires: Full Development System
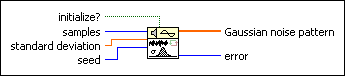
Generates a Gaussian-distributed, pseudorandom pattern whose statistical profile is (mu, sigma) = (0, s), where s is standard deviation.
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |





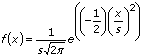
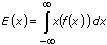
 , of the pseudorandom sequence:
, of the pseudorandom sequence: