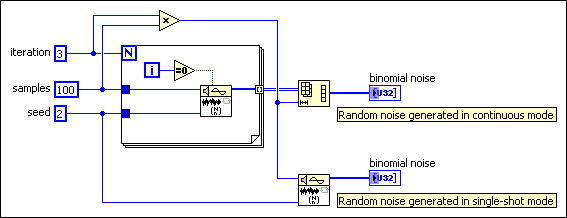
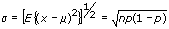Binomial Noise VI

Owning Palette: Signal Generation VIs

Requires: Full Development System

Generates a binomially-distributed, pseudorandom pattern whose values are the number of occurrences of an event, given the probability of that event occurring and the number of trials.

Details  

Add to the block diagram

Find on the palette

	initialize? controls the reseeding of the noise sample generator after the first call of the VI. If initialize? is TRUE, accepts a new state or new seed value and begins producing noise samples based on the new state or new seed value. If initialize? is FALSE, this VI maintains the initial internal seed state and resumes producing noise samples as a continuation of the previous noise sequence. The default is TRUE.
	samples specifies the number of samples contained in the output array. samples must be greater than 0. The default is 128.
	trials is the number of trials performed for each element of binomial noise. trials must be greater than or equal to zero. The default is 1.
	trial probability is the probability that a given trial is true (1). trial probability must be in the range [0, 1]. The default is 0.5.
	seed determines how to generate the internal seed state when initialize? is TRUE. If seed is greater than 0, this VI uses seed to generate the internal state directly. If seed is less than or equal to 0, this VI uses a random number to generate the internal state. seed must not be a multiple of 16384. If initialize? is FALSE, this VI ignores seed. The default is -1.
	binomial noise contains the binomially-distributed, pseudorandom pattern.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Binomial Noise Details

The Binomial Noise VI generates a binomially-distributed, pseudorandom pattern whose values are the number of occurrences of an event. The following equation defines the probability density function of the binomial noise:

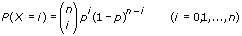
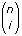where n is the number of trials, p is the trial probability, and equals 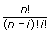. To generalize, P(X = i) is the probability that i of the n trials equals 1, and n – i equals zero. When n equals 1, the Binomial noise degenerates into Bernoulli noise.

The following equations define the mean value, µ, and the standard deviation value, , of the pseudorandom sequence:

µ = E{x} = np

You can use the initialize? input to generate a long random noise sequence block by block. The following block diagram shows two ways to generate identical 300-sample Binomial noise sequences with a seed of 2.

You also can use the Binomial Noise Waveform VI to generate a Binomial noise signal or the Discrete Random VI to generate random values from a binomial-distributed variate.