QZ Decomposition VI

Owning Palette: Linear Algebra VIs

Requires: Full Development System

Performs the QZ decomposition of a pair of square matrices. The data types you wire to the A and B inputs determine the polymorphic instance to use.

Details  

Use the pull-down menu to select an instance of this VI.

Select an instance Real QZ DecompositionComplex QZ Decomposition

Add to the block diagram

Find on the palette

Real QZ Decomposition

	A is a square real matrix.
	B is the second square real matrix.
	decomposition type specifies the type of decomposition to perform. 0 Generalized Hessenberg (default) 1 Generalized Schur
	order specifies how to order the generalized eigenvalues, Alpha and Beta. order is available only when decomposition type is Generalized Schur. The default is No Reorder. 0 No Reorder—Does not change the order of the generalized eigenvalues. 1 Real Ascending—Lists the generalized eigenvalues in ascending order according to the real parts. 2 Real Descending—Lists the generalized eigenvalues in descending order according to the real parts. 3 Magnitude Ascending—Lists the generalized eigenvalues in ascending order according to the magnitudes. 4 Magnitude Descending—Lists the generalized eigenvalues in descending order according to the magnitudes.
	Eigenvectors returns a complex matrix that contains the generalized eigenvectors in its columns.
	Q is an orthogonal matrix. When trans(Q) is the transpose matrix of Q, Q satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Z is an orthogonal matrix. When trans(Q) is the transpose matrix of Q, Z satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Alpha returns the numerators of the generalized eigenvalues of matrix pair (A,B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A,B).
	Beta returns the denominators of the generalized eigenvalues of matrix pair (A,B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A,B).
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Complex QZ Decomposition

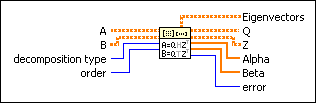
	A is a square complex matrix.
	B is the second square complex matrix.
	decomposition type specifies the type of decomposition to perform. 0 Generalized Hessenberg (default) 1 Generalized Schur
	order specifies how to order the generalized eigenvalues, Alpha and Beta. order is available only when decomposition type is Generalized Schur. The default is No Reorder. 0 No Reorder—Does not change the order of the generalized eigenvalues. 1 Real Ascending—Lists the generalized eigenvalues in ascending order according to the real parts. 2 Real Descending—Lists the generalized eigenvalues in descending order according to the real parts. 3 Magnitude Ascending—Lists the generalized eigenvalues in ascending order according to the magnitudes. 4 Magnitude Descending—Lists the generalized eigenvalues in descending order according to the magnitudes.
	Eigenvectors returns a complex matrix that contains the generalized eigenvectors in its columns.
	Q is a unitary matrix. When trans(Q) is the conjugate transpose matrix of Q, Q satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg or an upper triangular matrix if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Z is a unitary matrix. When trans(Q) is the conjugate transpose matrix of Q, Z satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg or an upper triangular matrix if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Alpha returns the numerators of the generalized eigenvalues of matrix pair (A,B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A,B).
	Beta returns the denominators of the generalized eigenvalues of matrix pair (A,B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A,B).
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

QZ Decomposition Details

The following expressions define the QZ decomposition of a matrix pair (A, B).

A = QHZ^H

B = QTZ^H

where A and B are n-by-n square matrices, Z^H is the conjugate transpose of matrix Z, T is an n-by-n upper triangular matrix, and H is an n-by-n upper Hessenberg matrix if the decomposition type is Generalized Hessenberg or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. Refer to the Hessenberg Decomposition VI for information about Hessenberg matrices.

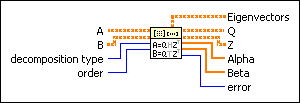
If B is singular, matrix pair (A, B) has an infinite generalized eigenvalue, in other words, Beta_i is zero. If A–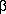B is singular for all and , matrix pair (A, B) is singular and has an indeterminate generalized eigenvalue, in other words, both Beta_i and Alpha_i are zeros. This VI cannot order the generalized eigenvalues if there are indeterminate generalized eigenvalues.