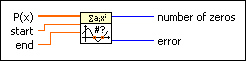
Polynomial Real Zeros Counter VI

Owning Palette: Polynomial VIs

Requires: Full Development System

Calculates the number of zeros of the real polynomial P(x) in a real interval defined by start and end without determining the values of the zeros.

Details  

Add to the block diagram

Find on the palette

	P(x) is an array that represents the polynomial. The first element of this array relates to the constant coefficient of P(x).
	start is the leftmost point of the interval. The default is 0.0.
	end is the rightmost point of the interval. The default is 0.0.
	number of zeros is the exact number of zeros of P(x) in the interval (start, end).
	error returns any error or warning from the VI. When start > end, the application interprets it as an error. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Polynomial Real Zeros Counter Details

This VI uses the Sturm algorithm to calculate the number of zeros. The Sturm algorithm deals with two situations. Let p(x) be a real polynomial in x and let p'(x) be the derivative of p(x). If d(x) denotes the greatest common divisor of p(x) and p'(x),

d(x) = gcd(p(x), p´(x))

so p(x) has multiple zeros, if d(x) is a nonconstant polynomial. In other words, the polynomial p(x)/d(x) has only single zeros.

Repeating this idea, you can combine the polynomial p(x) as the product of simple polynomials, each of which has single real zeros. The number of zeros of p(x) is equal to the sum of all zeros of the defined simple polynomials that have only single zeros.

To determine the number of zeros of a real polynomial p(x) with the single zero property, use the following Euclidean algorithm:

p(x) = q₁(x)p₁(x) – p₂(x)

p₁(x) = q₂(x)p₂(x) – p₃(x)

p_{r – 2}(x) = q_{r – 1}(x)p_{r – 1}(x) – p_r(x)

The Sturm's chain

(p(x), p₁(x), …, p_r(x))

determines two values W(start) and W(end). W(x) is the number of sign changes of the chain

(p(x), p₁(x), …, p_r(x))

The number of all zeros of p(x) is exactly equal to W(end)–W(start).

Note  If you are interested in all real zeros of a real polynomial, choose start = –max{(|a0| + … + |an–1|)/|an|, 1} and end = max{(|a0| + … + |an–1|)/|an|, 1} where a0, a1, …, an are the elements of the polynomial.