For a real polynomial, you can find the number of real roots of the polynomial over a certain interval by applying the Sturm function.
If
P0(x) = P(x)
and
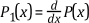
the following equation defines the Sturm function.
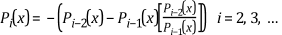
where Pi(x) is the Sturm function and
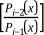
represents the quotient polynomial resulting from the division of Pi - 2(x) by Pi - 1(x).
You can calculate Pi(x) until it becomes a constant. For example, the following equations show the calculation of the Sturm function over the interval (-2, 1).
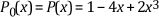
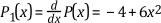
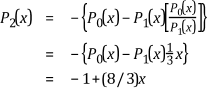
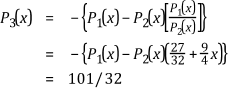
To evaluate the Sturm functions at the boundary of the interval (-2, 1), you do not have to calculate the exact values in the evaluation. You only need to know the signs of the values of the Sturm functions. The following table lists the signs of the Sturm functions for the interval (-2, 1).
| x | P0(x) | P1(x) | P2(x) | P3(x) | Number of Sign Changes |
|---|---|---|---|---|---|
| -2 | - | + | - | + | 3 |
| 1 | - | + | + | + | 1 |
In the previous table, notice the number of sign changes for each boundary. For x = -2, the evaluation of Pi(x) results in three sign changes. For x = 1, the evaluation of Pi(x) results in one sign change.
The difference in the number of sign changes between the two boundaries corresponds to the number of real roots that lie in the interval. For the calculation of the Sturm function over the interval (-2, 1), the difference in the number of sign changes is two, which means two real roots of polynomial P(x) lie in the interval (-2, 1). The following figure shows the result of evaluating P(x) over (-2, 1).
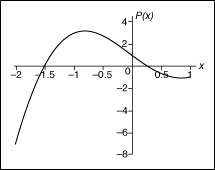
In the previous figure, the two real roots lie at approximately -1.5 and 0.26.