LU Factorization VI

Requires: Full Development System

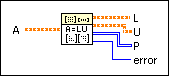
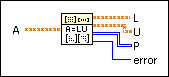
Performs the LU factorization of A so that PA = LU. Wire data to the A input to determine the polymorphic instance to use or manually select the instance.

Details Example

Use the pull-down menu to select an instance of this VI.

Add to the block diagram

Find on the palette

Real LU Factorization

	A is a real matrix.
	L is a lower triangular matrix with ones on the diagonal.
	U is an upper triangular matrix.
	P is a permutation matrix.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Complex LU Factorization

	A is a complex matrix.
	L is a complex, lower triangular matrix with 1+0i on the diagonal.
	U is a complex, upper triangular matrix.
	P is a permutation matrix.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

LU Factorization Details

The LU Factorization VI factors an m × n matrix A into the following types of matrices so that PA = LU:

L is an m × min(m, n) matrix. When m ≤ n, L is a lower triangular matrix with ones on the diagonal. When m > n, L is a lower trapezoidal matrix with ones on the diagonal.
U is a min(m, n) × n matrix. When m ≥ n, U is an upper triangular matrix. When m < n, U is an upper trapezoidal matrix.
P is an m × m permutation matrix, which serves as the identity matrix with some rows exchanged.

For a singular matrix, the VI completes the factorization and returns a warning, and there is at least one zero at the diagonal of U.

The following equation illustrates one useful property of LU factorization when A is a square matrix:

where det(A) is the determinant of A.

LU factorization serves as a key step for inverting a matrix, computing the determinant of a matrix, and solving a linear equation.

Example

Refer to the Linear Algebra Calculator VI in the labview\examples\Mathematics\Linear Algebra directory for an example of using the LU Factorization VI.

Open example Find related examples