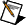
 |
Input Matrix is a square or rectangular, real matrix. The number of elements in the Known Vector must be equal to the rows of the Input Matrix. If the number of elements in the Known Vector does not match the rows of the Input Matrix, the VI sets the Solution Vector to an empty array and returns an error. When Input Matrix is singular, if the matrix type is General, the Solve Linear Equations VI finds the least-square solution. Otherwise, the VI returns an error.
|
 |
Known Vector is an array of known, dependent-variable values. The number of elements in the Known Vector must be equal to the rows of the Input Matrix. If the number of elements in the Known Vector does not match the rows of the Input Matrix, the VI sets the Solution Vector to an empty array and returns an error.
|
 |
matrix type is the type of Input Matrix. Knowing the type of Input Matrix can speed up the computation of the Solution Vector and can help you to avoid unnecessary computation, which could introduce numerical inaccuracy.
| 0 | General (default) | | 1 | Positive definite | | 2 | Lower triangular | | 3 | Upper triangular |
|
 |
Solution Vector is the solution X to AX = Y where A is the Input Matrix and Y is the Known Vector.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 |
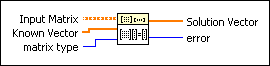
Input Matrix is a square or rectangular, real matrix. The number of rows in the Known Matrix must be equal to the rows of the Input Matrix. If the number of rows in the Known Matrix does not match the rows of the Input Matrix, the VI sets the Solution Matrix to an empty matrix and returns an error. When Input Matrix is singular, if the matrix type is General, the VI finds the least-square solution. Otherwise, the VI returns an error.
|
 |
Known Matrix is a matrix of known, dependent-variable values. Known Matrix must have the same number of rows as Input Matrix. If the number of rows in Known Matrix and Input Matrix are not equal, the VI sets Solution Matrix to an empty matrix and returns an error.
|
 |
matrix type is the type of Input Matrix. Knowing the type of Input Matrix can speed up the computation of the Solution Matrix and can help you to avoid unnecessary computation, which could introduce numerical inaccuracy.
| 0 | General (default) | | 1 | Positive definite | | 2 | Lower triangular | | 3 | Upper triangular |
|
 |
Solution Matrix returns the solution X to AX = Y where A is the Input Matrix and Y is the Known Matrix.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|

 |
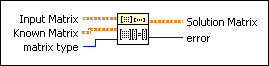
Input Matrix must be a nonsingular, square or rectangular, complex matrix. A nonsingular matrix is a matrix in which no row or column contains a linear combination of any other row or column, respectively. You cannot always determine beforehand whether the matrix is singular, especially with large systems. When Input Matrix is singular, if the matrix type is General, the VI finds the least-square solution. Otherwise, the VI returns an error.
|
 |
Known Vector is an array of known, dependent-variable values. The number of elements in Known Vector must match the row size of the Input Matrix. If the number of elements in Known Vector does not match the row size of Input Matrix, the VI sets Solution Vector to an empty array and returns an error.
|
 |
matrix type is the type of Input Matrix. Knowing the type of Input Matrix can speed up the computation of the Solution Vector and can help you to avoid unnecessary computation, which could introduce numerical inaccuracy.
| 0 | General (default) | | 1 | Positive definite | | 2 | Lower triangular | | 3 | Upper triangular |
|
 |
Solution Vector is the solution X to AX = Y where A is the Input Matrix and Y is the Known Vector.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|

 |
Input Matrix must be a nonsingular, square or rectangular, complex matrix. A nonsingular matrix is a matrix in which no row or column contains a linear combination of any other row or column, respectively. You cannot always determine beforehand whether the matrix is singular, especially with large systems. When Input Matrix is singular, if the matrix type is General, the VI finds the least-square solution. Otherwise, the VI returns an error.
|
 |
Known Matrix is a matrix of known, dependent-variable values. Known Matrix must have the same number of rows as Input Matrix. If the number of rows in Known Matrix and Input Matrix are not equal, the VI sets Solution Matrix to an empty matrix and returns an error.
|
 |
matrix type is the type of Input Matrix. Knowing the type of Input Matrix can speed up the computation of the Solution Matrix and can help you to avoid unnecessary computation, which could introduce numerical inaccuracy.
| 0 | General (default) | | 1 | Positive definite | | 2 | Lower triangular | | 3 | Upper triangular |
|
 |
Solution Matrix returns the solution X to AX = Y where A is the Input Matrix and Y is the Known Matrix.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
Let A be an m-by-n matrix that represents the Input Matrix, Y be the set of m coefficients in Known Vector, and X be the set of n elements in Solution Vector that solves the system
AX = Y
When m > n, the system has more equations than unknowns, so it is an over-determined system. The solution that satisfies AX = Y might not exist, so the VI finds the least-square solution X, which minimizes ||AX – Y||.
When m < n, the system has more unknowns than equations, so it is an under-determined system. It may have infinite solutions that satisfy AX = Y. The VI finds one of these solutions.
In the case of m = n, if A is a nonsingular matrix—no row or column is a linear combination of any other row or column, respectively—then you can solve the system for X by decomposing the input matrix A into its lower and upper triangular matrices, L and U, such that
AX = LZ = Y
and
Z = UX
can be an alternate representation of the original system. Notice that Z is also an n-element vector.
Triangular systems are easy to solve using recursive techniques. Consequently, when you obtain the L and U matrices from A, you can find Z from the LZ = Y system and X from the UX = Z system.
In the case of m  n, A can be decomposed to an orthogonal matrix Q and an upper triangular matrix R, so that A = QR. The linear system then can be represented by QRX = Y. You then can solve RX = QTY.
n, A can be decomposed to an orthogonal matrix Q and an upper triangular matrix R, so that A = QR. The linear system then can be represented by QRX = Y. You then can solve RX = QTY.
You can easily solve this triangular system to get x using recursive techniques.
 | Note You cannot always determine beforehand whether the matrix is singular, especially with large systems. The Solve Linear Equations VI detects singular matrices and returns an error, so you do not need to verify whether you have a valid system before using this VI. |
The numerical implementation of the matrix inversion is numerically intensive and, because of its recursive nature, is also highly sensitive to round-off error introduced by the floating-point numeric coprocessor. Although the computations use the maximum possible accuracy, the VI cannot always solve the system.
Solve Complex Linear Equations
Let A represent the m-by-n Input Matrix, Y represent the set of m elements in the Known Vector, and X represent the set of n elements in the Solution Vector that solves for the system
AX = Y
When m > n, the system has more equations than unknowns, so it is an over-determined system. Since the solution that satisfies AX = Y may not exist, the VI finds the least-square solution X, which minimizes ||AX – Y||.
When m < n, the system has more unknowns than equations, so it is an under-determined system. It might have infinite solutions that satisfy AX = Y. The VI then selects one of these solutions.
When m = n, if A is a nonsingular matrix—no row or column is a linear combination of any other row or column, respectively—then you can solve the system for X by decomposing the Input Matrix A into its lower and upper triangular matrices, L and U, such that
AX = LZ = Y
and
Z = UX
can be an alternate representation of the original system. Notice that Z is also an n-element vector.
Triangular systems are easy to solve using recursive techniques. Consequently, when you obtain the L and U matrices from A, you can find Z from the LZ = Y system and X from the UX = Z system.
When m  n, A can be decomposed to an orthogonal matrix Q, and an upper triangular matrix R, so that A = QR, and the linear system can be represented by QRX = Y. You then can solve RX = QHY. You can easily solve this triangular system to get X using recursive techniques.
n, A can be decomposed to an orthogonal matrix Q, and an upper triangular matrix R, so that A = QR, and the linear system can be represented by QRX = Y. You then can solve RX = QHY. You can easily solve this triangular system to get X using recursive techniques.
 | Note The numerical implementation of the matrix inversion is numerically intensive and, because of its recursive nature, is also highly sensitive to round-off error introduced by the floating-point numeric coprocessor. Although the computations use the maximum possible accuracy, the VI cannot always solve for the system. |
Refer to the Linear Algebra Calculator VI in the labview\examples\Mathematics\Linear Algebra directory for an example of using the Solve Linear Equations VI.
 Open example
Open example  Find related examples
Find related examples
 Add to the block diagram
Add to the block diagram Find on the palette
Find on the palette











 n, A can be decomposed to an orthogonal matrix Q and an upper triangular matrix R, so that A = QR. The linear system then can be represented by QRX = Y. You then can solve RX = QTY.
n, A can be decomposed to an orthogonal matrix Q and an upper triangular matrix R, so that A = QR. The linear system then can be represented by QRX = Y. You then can solve RX = QTY.