Euler Angles To Direction Cosines VI
Owning Palette: Geometry VIs
Requires: Full Development System
Converts Euler angles into a 3-by-3 matrix of direction cosines. The VI accepts both proper and Tait-Bryan angle types.

 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |





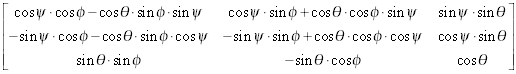
 (–
(– <
< 
 (0
(0 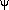 (–
(–