3D Cartesian Coordinate Rotation (Direction) VI

Owning Palette: Geometry VIs

Requires: Full Development System

Rotates a three-dimensional Cartesian coordinate in the counterclockwise direction using the direction method. Wire data to the X input to determine the polymorphic instance to use or manually select the instance.

Details  

Use the pull-down menu to select an instance of this VI.

Select an instance 3D Cartesian Coordinate Rotation (Direction) (Array)3D Cartesian Coordinate Rotation (Direction) (Scalar)

Add to the block diagram

Find on the palette

3D Cartesian Coordinate Rotation (Direction) (Array)

	X specifies the input x-coordinates.
	Y specifies the input y-coordinates.
	Z specifies the input z-coordinates.
	Rotation Matrix specifies the 3-by-3 direction cosine matrix. If rotation matrix type is Direction Cosines, each element in Rotation Matrix must be in the range of [-1, 1].
	rotation matrix type determines whether the Rotation Matrix contains the direction angles or the direction cosines. 0 Direction Angles (default)—Indicates that the Rotation Matrix contains the direction angles, or the angles between the x-, y-, and z-axes and the line segments from the origin to the input coordinates. 1 Direction Cosines—Indicates that the Rotation Matrix contains the direction cosines, or the cosines of the direction angles.
	X Out returns the rotated x-coordinates.
	Y Out returns the rotated y-coordinates.
	Z Out returns the rotated z-coordinates.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

3D Cartesian Coordinate Rotation (Direction) (Scalar)

	x is the real input x-component for the two-element vector.
	y is the real input y-component for the two-element vector.
	z specifies the input z-coordinate.
	Rotation Matrix specifies the 3-by-3 direction cosine matrix. If rotation matrix type is Direction Cosines, each element in Rotation Matrix must be in the range of [-1, 1].
	rotation matrix type determines whether the Rotation Matrix contains the direction angles or the direction cosines. 0 Direction Angles (default)—Indicates that the Rotation Matrix contains the direction angles, or the angles between the x-, y-, and z-axes and the line segments from the origin to the input coordinates. 1 Direction Cosines—Indicates that the Rotation Matrix contains the direction cosines, or the cosines of the direction angles.
	x out returns the rotated x-coordinate.
	y out returns the rotated y-coordinate.
	z out returns the rotated z-coordinate.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

3D Cartesian Coordinate Rotation (Direction) Details

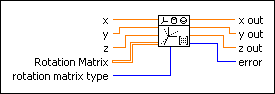
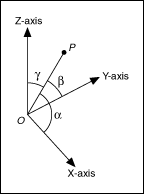
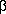For a point P, , , and 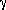are the direction angles of vector OP, as shown in the following illustration:

The cosines of the direction angles are direction cosines.

Before the rotation, the coordinate of point P is (x, y, z). After the rotation, the coordinate of point P is (x', y', z'), where

A is the Rotation Matrix defined by:

₁, ₁, and ₁ are the direction angles of the X'-axis to the X-, Y-, and Z-axes. ₂, ₂, and ₂ are the direction angles of the Y'-axis to the X-, Y-, and Z-axes. ₃, ₃, and ₃ are the direction angles of the Z'-axis to the X-, Y-, and Z-axes.