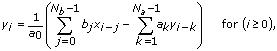|
initialize, when TRUE, initializes the internal state of the VI.
|
 |
x is the input signal to filter.
|
 |
Reverse Coefficients is the reverse coefficients of the filter design. This VI does not place any restrictions on the coefficient arrays. If both coefficient arrays are empty, the VI performs no filtering and sets Filtered X to the value of X.
|
 |
Forward Coefficients is the forward coefficients of the filter design.
|
 |
Initial X Conditions contains the most recent inputs. The most recent prior input should be the last element in the array. The number of elements in this array should be one less than the number of elements in the Forward Coefficients array.
|
 |
Initial Y Conditions contains the most recent outputs. The most recent output should be the last element in the array. The number of elements in this array should be one less than the number of elements in the Reverse Coefficients array.
|
 |
Filtered x contains the result of filtering the input sequence x by convolution.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 |
Final X Conditions contains the most recent inputs. You can use Final X Conditions as Initial X Conditions on the next call to this VI.
|
 |
Final Y Conditions contains the most recent outputs. You can use Final Y Conditions as Initial Y Conditions on the next call to this VI.
|
The IIR Filter with I.C. PtByPt VI obtains the elements of Filtered X using the following equation.
The filter initialization uses the following equations.
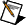
 Add to the block diagram
Add to the block diagram Find on the palette
Find on the palette