Owning Palette: Filters PtByPt VIs
Requires: Full Development System
Filters x using an equi-ripple highpass FIR filter model.
This VI is similar to the Equi-Ripple HighPass VI.
 | Note By default, reentrant execution is enabled in all Point By Point VIs. |
 Add to the block diagram |
 Find on the palette |
 |
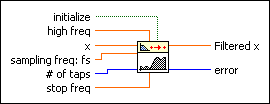
initialize, when TRUE, initializes the internal state of the VI. | ||
 |
high freq must be greater than stop freq and observe the Nyquist criterion. The default is 0.3 Hz. If high freq is less than or equal to stop freq or does not meet the Nyquist criterion, the VI sets Filtered x to zero and returns an error through the Parks-McClellan VI. | ||
|
x is the input signal to filter. | ||
|
sampling freq: fs is the frequency in Hz at which you want to sample x and must be greater than zero. The default is 1.0 Hz. | ||
 |
# of taps must be greater than 2. The default is 31. If # of taps is less than or equal to 2, the VI sets Filtered x to zero and returns an error through the Parks-McClellan VI.
|
||
|
stop freq must be greater than zero and observe the Nyquist criterion. The default is 0.2 Hz. If stop freq is less than or equal to zero or does not meet the Nyquist criterion, the VI sets Filtered x to zero and returns an error through the Parks-McClellan VI. | ||
 |
Filtered x contains the result of filtering the input sequence x by convolution. | ||
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
Generates a highpass FIR filter with equi-ripple characteristics using the Parks-McClellan algorithm and # of taps, stop freq, high freq, and sampling freq. The Equi-Ripple HighPass PtByPt VI then applies a linear-phase, highpass filter to x to obtain Filtered x.
The stopband of the filter goes from zero (DC) to the stop freq. The transition band goes from the stop freq to the high freq. The passband goes from the high freq to the Nyquist frequency.