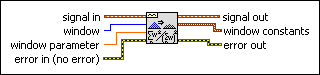
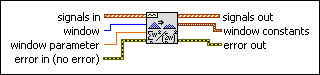
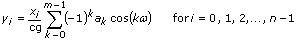Scaled Window VI

Owning Palette: Waveform Conditioning VIs

Requires: Full Development System

Applies a scaled window to the time-domain signal and outputs window constants for further analysis. Wire data to the signal in input to determine the polymorphic instance to use or manually select the instance.

Details  

Use the pull-down menu to select an instance of this VI.

Select an instance Scaled Window for 1 ChanScaled Window for N ChanScaled Window for 1 Chan (CDB)Scaled Window for N Chan (CDB)

Add to the block diagram

Find on the palette

Scaled Window for 1 Chan

	signal in is the signal to be windowed.
	window specifies the time-domain window used.
	window parameter is the beta parameter for a Kaiser window, the standard deviation for a Gaussian window, and the ratio, s, of the main lobe to the side lobe for a Dolph-Chebyshev window. If window is any other window, this VI ignores this input. The default value of window parameter is NaN, which sets beta to 0 for a Kaiser window, the standard deviation to 0.2 for a Gaussian window, and s to 60 for a Dolph-Chebyshev window.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	signal out is the windowed signal.
	window constants contains important constants for the selected window. eq noise BW is the equivalent noise bandwidth of the selected window. To compute the power in a given frequency span, divide a sum of individual FFT lines by eq noise BW. coherent gain is the inverse of the scaling factor applied due to the window.
	error out contains error information. This output provides standard error out functionality.

Scaled Window for N Chan

	signals in is the array of signals to window.
	window specifies the time-domain window used.
	window parameter is the beta parameter for a Kaiser window, the standard deviation for a Gaussian window, and the ratio, s, of the main lobe to the side lobe for a Dolph-Chebyshev window. If window is any other window, this VI ignores this input. The default value of window parameter is NaN, which sets beta to 0 for a Kaiser window, the standard deviation to 0.2 for a Gaussian window, and s to 60 for a Dolph-Chebyshev window.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	signals out returns the array of windowed signals.
	window constants contains important constants for the selected window. eq noise BW is the equivalent noise bandwidth of the selected window. To compute the power in a given frequency span, divide a sum of individual FFT lines by eq noise BW. coherent gain is the inverse of the scaling factor applied due to the window.
	error out contains error information. This output provides standard error out functionality.

Scaled Window for 1 Chan (CDB)

	signal in is the complex signal to be windowed.
	window specifies the time-domain window used.
	window parameter is the beta parameter for a Kaiser window, the standard deviation for a Gaussian window, and the ratio, s, of the main lobe to the side lobe for a Dolph-Chebyshev window. If window is any other window, this VI ignores this input. The default value of window parameter is NaN, which sets beta to 0 for a Kaiser window, the standard deviation to 0.2 for a Gaussian window, and s to 60 for a Dolph-Chebyshev window.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	signal out is the complex windowed signal.
	window constants contains important constants for the selected window. eq noise BW is the equivalent noise bandwidth of the selected window. To compute the power in a given frequency span, divide a sum of individual FFT lines by eq noise BW. coherent gain is the inverse of the scaling factor applied due to the window.
	error out contains error information. This output provides standard error out functionality.

Scaled Window for N Chan (CDB)

	signals in is the array of complex signals to window.
	window specifies the time-domain window used.
	window parameter is the beta parameter for a Kaiser window, the standard deviation for a Gaussian window, and the ratio, s, of the main lobe to the side lobe for a Dolph-Chebyshev window. If window is any other window, this VI ignores this input. The default value of window parameter is NaN, which sets beta to 0 for a Kaiser window, the standard deviation to 0.2 for a Gaussian window, and s to 60 for a Dolph-Chebyshev window.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	signals out returns the array of complex windowed signals.
	window constants contains important constants for the selected window. eq noise BW is the equivalent noise bandwidth of the selected window. To compute the power in a given frequency span, divide a sum of individual FFT lines by eq noise BW. coherent gain is the inverse of the scaling factor applied due to the window.
	error out contains error information. This output provides standard error out functionality.

Scaled Window Details

The windowed time-domain signal is scaled so that when the power or amplitude spectrum of the windowed waveform is computed, all windows provide the same level within the accuracy constraints of the window. This VI also returns important window constants for the selected window. These constants are useful when you use VIs that perform computations on the power spectrum, such as the Power & Frequency Estimate VI.

Defining Equations

All cosine windows without scaling are defined by the following equation.

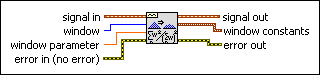
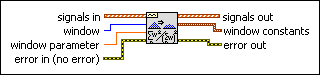
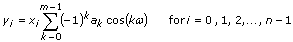
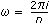where , n is the number of elements in X, and m is the number of elements in the window coefficient array a[].

For this VI, the preceding equation is modified to include division by the coherent gain (cg), as shown in the following equation.

Coefficients and Window Parameters for the Different Window Types

This section provides information about the a coefficients and window parameters for each window type available in this VI. Each window type has the following window parameters:

• coherent gain (cg)
• equivalent noise bandwidth (enbw)
• 6dB bandwidth (6dB BW)

Rectangle
a[] is empty because no window is applied.	cg = 1
The window equation is yi = xi	enbw = 1
	6dB BW = 1.21
Hanning
a0 = 0.5	cg = 0.5
a1 = 0.5	enbw = 1.5
	6dB BW = 2.0
Hamming
a0 = 0.54	cg = 0.54
a1 = 0.46	enbw = 1.362826
	6dB BW = 1.82
Blackman-Harris
a0 = 0.42323	cg = 0.42323
a1 = 0.49755	enbw = 1.708538
a2 = 0.07922	6dB BW = 2.27
Exact Blackman
a0 = 0.42659071367153911200	cg = 0.42659071367
a1 = 0.49656061908856408100	enbw = 1.693699
a2 = 0.07684866723989682010	6dB BW = 2.25
Blackman
a0 = 0.42	cg = 0.42
a1 = 0.5	enbw = 1.726757
a2 = 0.08	6dB BW = 2.3
Flat Top
a0 = 0.215578948	cg = 0.215578948
a1 = 0.41663158	enbw = 3.770246506303
a2 = 0.277263158	6dB BW = 4.58
a3 = 0.083578947
a4 = 0.006947368
4 Term B-Harris
a0 = 0.35875	cg = 0.35875
a1 = 0.48829	enbw = 2.004353
a2 = 0.14128	6dB BW = 2.67
a3 = 0.01168
7 Term B-Harris
a0 = 0.27105140069342415	cg = 0.27105140069342415
a1 = 0.43329793923448606	enbw = 2.631905
a2 = 0.21812299954311062	6dB BW = 3.5
a3 = 0.065925446388030898
a4 = 0.010811742098372268
a5 = 7.7658482522509342E-4
a6 = 1.3887217350903198E-5
Low Sidelobe
a0 = 0.323215218	cg = 0.323215218
a1 = 0.471492057	enbw = 2.215350782519
a2 = 0.17553428	6dB BW = 2.95
a3 = 0.028497078
a4 = 0.001261367