In many applications, you can allow the gain in the passband to vary slightly from unity. This variation in the passband is the passband ripple, or the difference between the actual gain and the desired gain of unity. In practice, the stopband attenuation cannot be infinite, and you must specify a value with which you are satisfied. Measure both the passband ripple and the stopband attenuation in decibels (dB). The following equation defines a decibel.
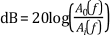
where log denotes the base 10 logarithm, Ai(f) is the amplitude at a particular frequency f before filtering, and A0(f) is the amplitude at a particular frequency f after filtering.
When you know the passband ripple or stopband attenuation, you can use the previous equation to determine the ratio of input and output amplitudes. The ratio of the amplitudes shows how close the passband or stopband is to the ideal. For example, for a passband ripple of -0.02 dB, the previous equation yields the following set of equations.
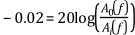
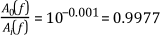
The previous two equations show that the ratio of input and output amplitudes is close to unity, which is the ideal for the passband.
Practical filter design attempts to approximate the ideal desired magnitude response, subject to certain constraints. The following table compares the characteristics of ideal filters and practical filters.
| Characteristic | Ideal Filters | Practical Filters |
|---|---|---|
| Passband | Flat and constant | Might contain ripples |
| Stopband | Flat and constant | Might contain ripples |
| Transition band | None | Have transition regions |
Practical filter design involves compromise, allowing you to emphasize a filter characteristic you want at the expense of a characteristic you do not want. The compromises you can make depend on whether the filter is an FIR or IIR filter and the design algorithm.