A set of vectors x1, x2, …, xn is linearly dependent only if there exist scalars a1, a2, …, an, not all zero, such that
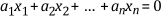
In simpler terms, if one of the vectors can be written in terms of a linear combination of the others, the vectors are linearly dependent.
If the only set of ai for which the previous equation holds is a1 = 0, a2 = 0, …, an = 0, the set of vectors x1, x2, …, xn is linearly independent. So in this case, none of the vectors can be written in terms of a linear combination of the others. Given any set of vectors, the previous equation always holds for a1 = 0, a2 = 0, …, an = 0. Therefore, to show the linear independence of the set, you must show that a1 = 0, a2 = 0, …, an = 0 is the only set of ai for which the previous equation holds.
For example, first consider the vectors
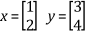
a1 = 0 and a2 = 0 are the only values for which the relation a1x + a2y = 0 holds true. Therefore, these two vectors are linearly independent of each other. Now consider the vectors
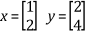
If a1 = -2 and a2 = 1, a1x + a2y = 0. Therefore, these two vectors are linearly dependent on each other. You must understand this definition of linear independence of vectors to fully appreciate the concept of the rank of the matrix.