You can use the Hilbert transform to isolate the slowly varying envelope from an oscillating signal.
For the signal of the equation
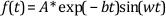
the rapidly oscillating component is sin(wt) and the envelope is the exponential A*exp(-bt).
The Hilbert transform of f(t) phase shifts the oscillatory component by 90 degrees in the following equation:
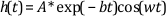
If the values of f(t) and h(t) are in arrays, calculate the envelope function with |f(t) + ih(t)|.