Measuring the frequency content of a signal requires digitalization of a continuous signal. To use digital signal processing techniques, you must first convert an analog signal into its digital representation. In practice, the conversion is implemented by using an analog-to-digital (A/D) converter. Consider an analog signal x(t) that is sampled every Δt seconds. The time interval Δt is the sampling interval or sampling period. Its reciprocal, 1/Δt, is the sampling frequency, with units of samples/second. Each of the discrete values of x(t) at t = 0, Δt, 2Δt, 3Δt, and so on, is a sample. Thus, x(0), x(Δt), x(2Δt), …, are all samples. The signal x(t) thus can be represented by the following discrete set of samples.
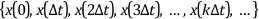
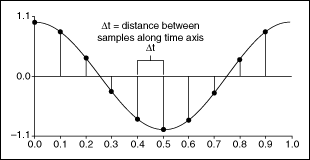
The following figure shows an analog signal and its corresponding sampled version. The sampling interval is Δt. The samples are defined at discrete points in time.
The following notation represents the individual samples.
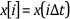
for i= 0, 1, 2, …
If N samples are obtained from the signal x(t), then you can represent x(t) by the following sequence:
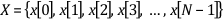
The preceding sequence representing x(t) is the digital representation, or the sampled version, of x(t). The sequence X = {x[i]} is indexed on the integer variable i and does not contain any information about the sampling rate. So knowing only the values of the samples contained in X gives you no information about the sampling frequency.
One of the most important parameters of an analog input system is the frequency at which the DAQ device samples an incoming signal. The sampling frequency determines how often an A/D conversion takes place. Sampling a signal too slowly can result in an aliased signal.