Rational polynomial functions have many applications, such as filter design, system theory, and digital image processing. In particular, rational polynomial functions provide the most common way of representing the z-transform. A rational polynomial function takes the form of the division of two polynomials, as shown by the following equation.
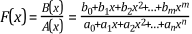
where F(x) is the rational polynomial, B(x) is the numerator polynomial, A(x) is the denominator polynomial, and A(x) cannot equal zero.
The roots of B(x) are the zeros of F(x). The roots of A(x) are the poles of F(x).