In the analog world, a signal frequency is measured in hertz (Hz), or cycles per second. But the digital system often uses a digital frequency, which is the ratio between the analog frequency and the sampling frequency, as shown by the following equation.
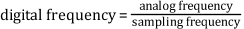
The digital frequency is known as the normalized frequency and is measured in cycles per sample.
The normalized frequency ranges from 0.0 to 1.0, which corresponds to a real frequency range of 0 to the sampling frequency fs. The normalized frequency also wraps around 1.0 so a normalized frequency of 1.1 is equivalent to 0.1. For example, a signal sampled at the Nyquist rate of fs/2 means it is sampled twice per cycle, that is, two samples/cycle. This sampling rate corresponds to a normalized frequency of 1/2 cycles/sample = 0.5 cycles/sample. The reciprocal of the normalized frequency, 1/f, gives you the number of times the signal is sampled in one cycle, that is, the number of samples per cycle.
If you are used to working in frequency units of cycles, you can convert cycles to cycles per sample by dividing cycles by the number of samples generated.
You need only divide the frequency in cycles by the number of samples. For example, a frequency of two cycles is divided by 50 samples, resulting in a normalized frequency of f = 1/25 cycles/sample. This means that it takes 25, the reciprocal of f, samples to generate one cycle of the sine wave.
However, you might need to use frequency units of Hz, cycles per second. If you need to convert from Hz to cycles per sample, divide the frequency in Hz by the sampling rate given in samples per second, as shown in the following equation.
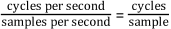
For example, you divide a frequency of 60 Hz by a sampling rate of 1,000 Hz to get the normalized frequency of f = 0.06 cycles/sample. Therefore, it takes almost 17, or 1/0.06, samples to generate one cycle of the sine wave.