A univariate polynomial is a mathematical expression involving a sum of powers in one variable multiplied by coefficients. The following equation shows the general form of an nth-order polynomial.
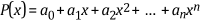
where P(x) is the nth-order polynomial, the highest power n is the order of the polynomial if an ≠ 0, a0, a1, …, an are the constant coefficients of the polynomial and can be either real or complex.
You can rewrite the previous equation in its factored form, as shown in the following equation.
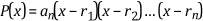
where r1, r2, …, rn are the roots of the polynomial.
The root ri of P(x) satisfies the following equation.
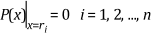
In general, P(x) might have repeated roots, such that the following equation is true.
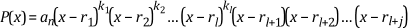
The following conditions are true for the previous equation:
- r1, r2, …, rl are the repeated roots of the polynomial
- ki is the multiplicity of the root ri, i = 1, 2, …, l
- rl + 1, rl + 2, …, rl + j are the non-repeated roots of the polynomial
- k1 + k2 + … + kl + j = n
A polynomial of order n must have n roots. If the polynomial coefficients are all real, the roots of the polynomial are either real or complex conjugate numbers.