The discrete Fourier transform (DFT) establishes the relationship between the samples of a signal in the time domain and their representation in the frequency domain. The DFT is widely used in the fields of spectral analysis, applied mechanics, acoustics, medical imaging, numerical analysis, instrumentation, and telecommunications. The following figure shows how to use the DFT to transform data from the time domain into the frequency domain.
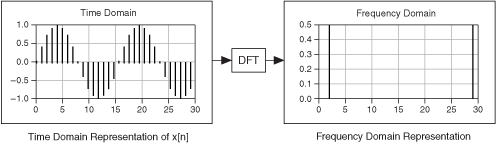
Suppose you obtained N samples of a signal from a DAQ device. If you apply the DFT to N samples of this time-domain representation of the signal, the result also is of length N samples, but the information it contains is of the frequency-domain representation.