The power spectrum shows power as the mean squared amplitude at each frequency line but includes no phase information. Because the power spectrum loses phase information, you might want to use the fast Fourier transform (FFT) to view both the frequency and the phase information of a signal.
The phase information the FFT provides is the phase relative to the start of the time-domain signal. Therefore, you must trigger from the same point in the signal to obtain consistent phase readings. A sine wave shows a phase of -90° at the sine wave frequency. A cosine wave shows a 0° phase. Usually, the primary area of interest for analysis applications is either the relative phases between components or the phase difference between two signals acquired simultaneously. You can view the phase difference between two signals by using some of the advanced FFT functions.
The FFT produces a two-sided spectrum in complex form with real and imaginary parts. You must scale and convert the two-sided spectrum to polar form to obtain magnitude and phase. The frequency axis of the polar form is identical to the frequency axis of the two-sided power spectrum. The amplitude of the FFT is related to the number of points in the time-domain signal. Use the following equations to compute the amplitude and phase versus frequency from the FFT.
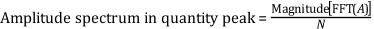
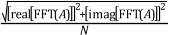
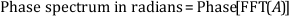
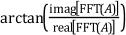
where the arctangent function returns values of phase between -π and +π, a full range of 2π radians.
The two-sided amplitude spectrum actually shows half the peak amplitude at the positive and negative frequencies. To convert to the single-sided form, multiply each frequency, other than DC, by two and discard the second half of the array. The units of the single-sided amplitude spectrum are then in quantity peak and give the peak amplitude of each sinusoidal component making up the time-domain signal.
To obtain the single-sided phase spectrum, discard the second half of the array.