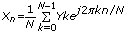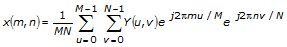Inverse FFT VI
Owning Palette: Transforms VIs
Requires: Full Development System
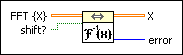
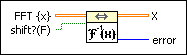
Computes the inverse discrete Fourier transform (IDFT) of the input sequence FFT {X}. You must manually select the polymorphic instance you want to use.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |








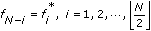 ,
, to perform the inverse real FFT, where
to perform the inverse real FFT, where  means the floor operation.
means the floor operation.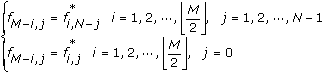
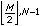 to perform the 2D inverse real FFT, where
to perform the 2D inverse real FFT, where