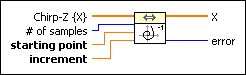
Inverse Chirp Z Transform VI

	Chirp-Z {X} is the complex valued input sequence. The length of Chirp-Z {x} must be greater than or equal to # of samples.
	# of samples specifies the length of X. # of samples must be less than or equal to the length of Chirp-Z {X}. If # of samples is less than or equal to 0, the VI sets # of samples to the length of Chirp-Z {X}. The default is –1.
	starting point is the point at which to begin evaluating the Chirp-Z transform and is best described by the equation in the details section. If starting point is 0, the VI returns an error.
	increment is the increment between each point to evaluate for the Chirp-Z transform. increment cannot be 0. To avoid singular cases of the inverse Chirp-Z transform, increment must be different from e^2πjk/L where k = 0, 1, …,L–1 L = 1, 2,…,N–1 and N is # of samples.
	X is the inverse Chirp-Z transform of Chirp-Z {X}.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Inverse Chirp Z Transform Details

If Y represents the sequence Chirp-Z {X}, the following equation shows how the VI performs the Chirp-Z transform to obtain the sequence X.

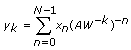
for k = 0, 1, …, M—1, where N is the length of X (# of samples), M is the length of Chirp-Z {X}, A is the starting point, W is the increment, X_n is the n^th element of X, and y_k is the k^th element of Chirp-Z {X}.

The inverse Chirp-Z transform computes the sequence X from Chirp-Z {X}. This VI employs a convolution-based method to implement this transform according to the following equations.

x_n=h_n*m_n

with

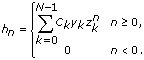
where

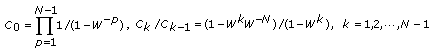
and

z_k=0, 1, …, N—1

m_n can be obtained from its z-transform M(z):

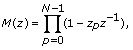
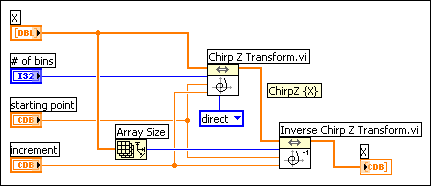
The following block diagram illustrates using the Inverse Chirp-Z Transform VI to compute the inverse Chirp-Z transform of some Chirp Z transformed signal.