Inverse Fast Hilbert Transform VI

Owning Palette: Transforms VIs

Requires: Full Development System

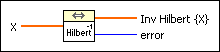
Computes the inverse fast Hilbert transform of the input sequence X using Fourier identities.

Details  

Add to the block diagram

Find on the palette

	X is the first input sequence.
	Inv Hilbert {X} is the inverse Hilbert Transform of the input signal X.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Inverse Fast Hilbert Transform Details

The inverse Hilbert transform of a function h(t) is defined as

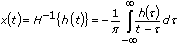
Using the definition of the Hilbert transform

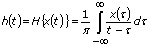
you can obtain the inverse Hilbert transform by negating the forward Hilbert transform

x(t) = H^–1{h(t)} = –H{h(t)}

Therefore, the Inverse Fast Hilbert Transform VI performs the discrete implementation of the inverse Hilbert transform with the aid of the Hilbert transform by taking the following steps.

1. Hilbert transform the input sequence X
   Y = H{X}.
2. Negate Y to obtain the inverse Hilbert transform
   H^–1{X} = –Y.

The Hilbert transform works best with AC coupled, band-limited signals.