 |
operation A specifies the operation the VI performs on matrix A in the Sylvester equation.
| 0 | not transposed (default)—op(A) = A | | 1 | transposed—op(A) = transpose of A |
|
 |
A contains matrix A in the Sylvester equation. A must be a square matrix or upper quasi-triangular matrix in canonical Schur form.
|
 |
B contains matrix B in the Sylvester equation. B must be a square matrix or upper quasi-triangular matrix in canonical Schur form.
|
 |
C contains matrix C in the Sylvester equation.
|
 |
sign specifies the form of the Sylvester equation.
| 0 | plus (default)—op(A)X + Xop(B) = aC | | 1 | minus—op(A)X – Xop(B) = aC |
|
 |
operation B specifies the operation the VI performs on matrix B in the Sylvester equation.
| 0 | not transposed (default)—op(B) = B | | 1 | transposed—op(B) = transpose of B |
|
 |
matrix type is the type of A and B. Specify types for A and B to speed up the computation of X and avoid unnecessary computation.
| 0 | General | | 3 | Upper Triangular (default) |
|
 |
X returns the solution of the Sylvester equation.
|
 |
scale returns the scaling factor a of the Sylvester equation.
|
 |
perturbed indicates whether the VI uses perturbed values to solve the equation. When perturbed is TRUE, the eigenvalues of A and B are common or close and indicate the solution of the Sylvester equation is not unique.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 |
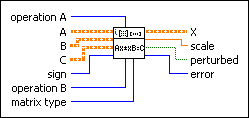
operation A specifies the operation the VI performs on matrix A in the Sylvester equation.
| 0 | not transposed (default)—op(A) = A | | 1 | transposed—op(A) = conjugate transpose of A |
|
 |
A contains matrix A in the Sylvester equation. A must be a square or upper-triangular matrix.
|
 |
B contains matrix B in the Sylvester equation. B must be a square or upper-triangular matrix.
|
 |
C contains matrix C in the Sylvester equation.
|
 |
sign specifies the form of the Sylvester equation.
| 0 | plus (default)—op(A)X + Xop(B) = aC | | 1 | minus—op(A)X – Xop(B) = aC |
|
 |
operation B specifies the operation the VI performs on matrix B in the Sylvester equation.
| 0 | not transposed (default)—op(B) = B | | 1 | transposed—op(B) = conjugate transpose of B |
|
 |
matrix type is the type of A and B. Specify types for A and B to speed up the computation of X and avoid unnecessary computation.
| 0 | General | | 3 | Upper Triangular (default) |
|
 |
X returns the solution of the Sylvester equation.
|
 |
scale returns the scaling factor a of the Sylvester equation.
|
 |
perturbed indicates whether the VI uses perturbed values to solve the equation. When perturbed is TRUE, the eigenvalues of A and B are common or close and indicate the solution of the Sylvester equation is not unique.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 Add to the block diagram
Add to the block diagram Find on the palette
Find on the palette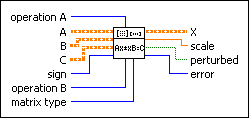









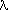 ±
±  ≠ 0, where
≠ 0, where