Matrix Characteristic Polynomial VI
Owning Palette: Linear Algebra VIs
Requires: Full Development System
Computes the characteristic polynomial of Input Matrix. Wire data to the Input Matrix input to determine the polymorphic instance to use or manually select the instance.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |







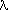 ) = det(
) = det(