Legendre Polynomial VI

Owning Palette: Orthogonal & Non-orthogonal Polynomials VIs

Requires: Full Development System

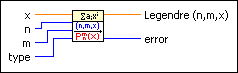
Calculates the associated Legendre polynomial of degree n and order m at point x.

Details  

Add to the block diagram

Find on the palette

	x is a real number between -1 and 1.
	n is the degree of the Legendre polynomial. n must be nonnegative.
	m is the order of the Legendre polynomial. m must be nonnegative and less than or equal to n.
	type specifies the type of Legendre polynomial. 0 Standard (default)—Computes the associated Legendre function. 1 Semi-Normalized—Computes the semi-normalized Legendre function. 2 Normalized—Computes the normalized associated Legendre function.
	Legendre (n,m,x) returns the value of the associated Legendre polynomial of degree n and order m at point x.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Legendre Polynomial Details

The associated Legendre polynomial of degree n and order m is the solution of the following associated Legendre differential equation.

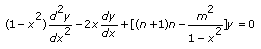
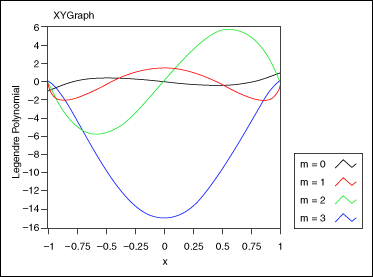
The following graph shows four associated Legendre polynomials of degree 3 (n=3).