 |
A is a matrix with m rows and p columns.
|
 |
B is a matrix with n rows and p columns.
|
 |
singular values only? specifies whether to compute only the generalized singular values. The default is FALSE. When singular values only? is TRUE, the VI computes only Singular Values.
|
 |
SVD Option specifies how the VI performs the decomposition.
| 0 | Thin (default)—Decomposes matrix A as the multiplication of matrix U (m x min(m,p)), C (min(m,p) x p) and transpose of R (p x p). Decomposes matrix B as the multiplication of matrix V (n x min(n,p)), S (min(n,p) x p) and transpose of R (p x p). | | 1 | Full—Decomposes matrix A as the multiplication of matrix U (m x m), C (m x p) and transpose of R (p x p). Decomposes matrix B as the multiplication of matrix V (n x n), S (n x p) and transpose of R (p x p). |
|
 |
Singular Values returns the generalized singular values of matrix pair (A,B).
|
 |
Matrix U returns the U matrix of the GSVD results.
|
 |
Matrix V returns the V matrix of the GSVD results.
|
 |
Matrix C returns the C matrix of the GSVD results.
|
 |
Matrix S returns the S matrix of the GSVD results.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 |
Matrix R returns the R matrix of the GSVD results.
|
 |
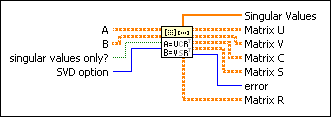
A is a matrix with m rows and p columns.
|
 |
B is a matrix with n rows and p columns.
|
 |
singular values only? specifies whether to compute only the generalized singular values. The default is FALSE. When singular values only? is TRUE, the VI computes only Singular Values.
|
 |
SVD Option specifies how the VI performs the decomposition.
| 0 | Thin (default)—Decomposes matrix A as the multiplication of matrix U (m x min(m,p)), C (min(m,p) x p) and transpose of R (p x p). Decomposes matrix B as the multiplication of matrix V (n x min(n,p)), S (min(n,p) x p) and transpose of R (p x p). | | 1 | Full—Decomposes matrix A as the multiplication of matrix U (m x m), C (m x p) and transpose of R (p x p). Decomposes matrix B as the multiplication of matrix V (n x n), S (n x p) and transpose of R (p x p). |
|
 |
Singular Values returns the generalized singular values of matrix pair (A,B).
|
 |
Matrix U returns the U matrix of the GSVD results.
|
 |
Matrix V returns the V matrix of the GSVD results.
|
 |
Matrix C returns the C matrix of the GSVD results.
|
 |
Matrix S returns the S matrix of the GSVD results.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 |
Matrix R returns the R matrix of the GSVD results.
|
The following expressions define the generalized singular value decomposition of a matrix pair (A,B).
 Add to the block diagram
Add to the block diagram Find on the palette
Find on the palette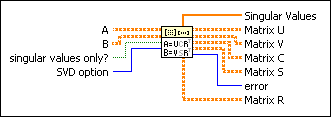








 , then the first k diagonal elements of matrix C�C + S�S are ones and all of the other elements are zeros. The square roots of the first k diagonal elements of C�C and S�S determine the numerators and denominators of the generalized singular values, respectively.
, then the first k diagonal elements of matrix C�C + S�S are ones and all of the other elements are zeros. The square roots of the first k diagonal elements of C�C and S�S determine the numerators and denominators of the generalized singular values, respectively.