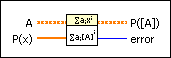
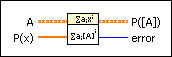
Evaluate Polynomial with Matrix VI

Owning Palette: Polynomial VIs

Requires: Full Development System

Evaluates the polynomial P(x) with matrix A. The data types you wire to the P(x) and A inputs determine the polymorphic instance to use.

Details  

Use the pull-down menu to select an instance of this VI.

Select an instance Evaluate Polynomial with Matrix (DBL)Evaluate Polynomial with Matrix (CDB)

Add to the block diagram

Find on the palette

Evaluate Polynomial with Matrix (DBL)

	A is a square matrix of real values. A acts as the independent variable of P(x). If A is not square, the VI sets P([A]) to an empty array and returns an error.
	P(x) contains the real polynomial coefficients in ascending order of power.
	P([A]) returns the evaluation of the real polynomial P(x) at the real values A contains.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Evaluate Polynomial with Matrix (CDB)

	A is a square matrix of complex values. A acts as the independent variable of P(x). If A is not square, the VI sets P([A]) to an empty array and returns an error.
	P(x) contains the complex polynomial coefficients in ascending order of power.
	P([A]) returns the evaluation of the complex polynomial P(x) at the complex values A contains.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Evaluate Polynomial with Matrix Details

The VI evaluates the polynomial P(x) with the square matrix A. For example, the following polynomial defines the second-order polynomial described by the three-element array P[0…2]:

P[2]x² + P[1]x + p[0]

The evaluation of the preceding polynomial by the VI yields the following result:

P([A]) = P[2]A² + P[1]A + P[0]I

where I is the identity matrix and the same size as A.