Create Real Matrix From Eigenvalues VI
Owning Palette: Linear Algebra VIs
Requires: Full Development System
Generates a real matrix from Eigenvalues.
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
Owning Palette: Linear Algebra VIs
Requires: Full Development System
Generates a real matrix from Eigenvalues.

 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
 |
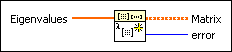
Eigenvalues contains the eigenvalues from which you want to create Matrix. Eigenvalues must be real or conjugate pairs. |
 |
Matrix returns the real matrix whose eigenvalues are specified by Eigenvalues. |
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
This VI generates the Matrix in the following form:
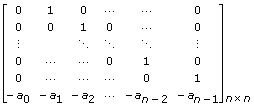
where n is the length of Eigenvalues and a0, a1, …, an – 1 are the coefficients of the polynomial P(x).
The following equation defines P(x):
P(x) = (x – 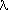 0)(x –
0)(x – 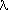 1)···(x –
1)···(x – 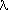 n – 1) = a0 + a1x + a2x2 + … + an – 1xn – 1 + xn
n – 1) = a0 + a1x + a2x2 + … + an – 1xn – 1 + xn
where 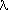 0,
0, 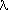 1, …,
1, …, 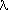 n – 1 are the elements in Eigenvalues.
n – 1 are the elements in Eigenvalues.