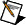|
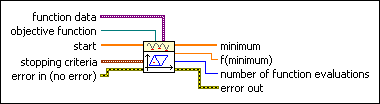
function data contains static data that the user-defined function needs at run time.
|
 |
objective function is a reference to the VI that implements the function to optimize. Create this VI by starting from the VI template located at labview\vi.lib\gmath\NumericalOptimization\ucno_objective function template.vit.
 Open template Open template
|
 |
start is a point in n dimension at which the optimization process starts.
|
 |
stopping criteria is the collection of conditions that terminate the optimization. If (function tolerance AND parameter tolerance AND gradient tolerance) OR max iterations OR max function calls then optimization terminates.
 |
function tolerance is the relative change in function value and is defined as abs(current f – prev f)/(abs(curr f)+machine eps). If the relative change in the function value falls below function tolerance, the optimization terminates.
|
 |
parameter tolerance is the relative change in parameter values and is defined as abs(current p – prev p)/(abs(curr p)+machine eps). If the relative change of all the parameter values falls below parameters tolerance, the optimization terminates.
|
 |
gradient tolerance is the 2–norm of the gradient. If the 2–norm of the gradient falls below gradient tolerance, the optimization terminates.
|
 |
max iterations is the largest number of iterations of the major loop of the optimization. If the number of major loop iterations exceeds max iterations, the optimization terminates.
|
 |
max function calls is the largest number of objective function calls allowed before terminating the optimization process.
|
 |
max time (sec) is the maximum amount of time LabVIEW allows between the start and the end of the optimization process. The default is –1. –1 indicates never to time out.
|
|
 |
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
|
 |
minimum is the determined local minimum in n dimension.
|
 |
f(minimum) is the function value of f(X) at the determined minimum.
|
 |
number of function evaluations is the number of times the objective function was called in the optimization process.
|
 |
error out contains error information. This output provides standard error out functionality.
|
 |
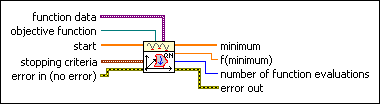
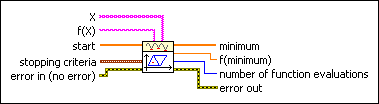
X is an array of strings representing the x variables.
|
 |
f(X) is the string representing the function of the x variables. The formulas can contain any number of valid variables.
|
 |
start is a point in n dimension at which the optimization process starts.
|
 |
stopping criteria is the collection of conditions that terminate the optimization. If (function tolerance AND parameter tolerance AND gradient tolerance) OR max iterations OR max function calls then optimization terminates.
 |
function tolerance is the relative change in function value and is defined as abs(current f – prev f)/(abs(curr f)+machine eps). If the relative change in the function value falls below function tolerance, the optimization terminates.
|
 |
parameter tolerance is the relative change in parameter values and is defined as abs(current p – prev p)/(abs(curr p)+machine eps). If the relative change of all the parameter values falls below parameters tolerance, the optimization terminates.
|
 |
gradient tolerance is the 2–norm of the gradient. If the 2–norm of the gradient falls below gradient tolerance, the optimization terminates.
|
 |
max iterations is the largest number of iterations of the major loop of the optimization. If the number of major loop iterations exceeds max iterations, the optimization terminates.
|
 |
max function calls is the largest number of objective function calls allowed before terminating the optimization process.
|
 |
max time (sec) is the maximum amount of time LabVIEW allows between the start and the end of the optimization process. The default is –1. –1 indicates never to time out.
|
|
 |
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
|
 |
minimum is the determined local minimum in n dimension.
|
 |
f(minimum) is the function value of f(X) at the determined minimum.
|
 |
number of function evaluations is the number of times the objective function was called in the optimization process.
|
 |
error out contains error information. This output provides standard error out functionality.
|
 |
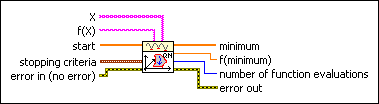
function data contains static data that the user-defined function needs at run time.
|
 |
objective function is a reference to the VI that implements the function to optimize. Create this VI by starting from the VI template located at labview\vi.lib\gmath\NumericalOptimization\ucno_objective function template.vit.
 Open template Open template
|
 |
start is a point in n dimension at which the optimization process starts.
|
 |
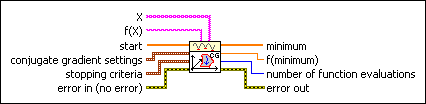
conjugate gradient settings
 |
gradient method specifies the algorithm used to compute the derivatives. A value of 0 represents the Fletcher Reeves method. A value of 1 represents the Polak Ribiere method. The default is 0.
|
 |
line minimization A value of 0 represents an algorithm without usage of the derivatives. A value of 1 represents an algorithm with usage of the derivatives. The default is 0.
|
|
 |
stopping criteria is the collection of conditions that terminate the optimization. If (function tolerance AND parameter tolerance AND gradient tolerance) OR max iterations OR max function calls then optimization terminates.
 |
function tolerance is the relative change in function value and is defined as abs(current f – prev f)/(abs(curr f)+machine eps). If the relative change in the function value falls below function tolerance, the optimization terminates.
|
 |
parameter tolerance is the relative change in parameter values and is defined as abs(current p – prev p)/(abs(curr p)+machine eps). If the relative change of all the parameter values falls below parameters tolerance, the optimization terminates.
|
 |
gradient tolerance is the 2–norm of the gradient. If the 2–norm of the gradient falls below gradient tolerance, the optimization terminates.
|
 |
max iterations is the largest number of iterations of the major loop of the optimization. If the number of major loop iterations exceeds max iterations, the optimization terminates.
|
 |
max function calls is the largest number of objective function calls allowed before terminating the optimization process.
|
 |
max time (sec) is the maximum amount of time LabVIEW allows between the start and the end of the optimization process. The default is –1. –1 indicates never to time out.
|
|
 |
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
|
 |
minimum is the determined local minimum in n dimension.
|
 |
f(minimum) is the function value of f(X) at the determined minimum.
|
 |
number of function evaluations is the number of times the objective function was called in the optimization process.
|
 |
error out contains error information. This output provides standard error out functionality.
|
 |
X is an array of strings representing the x variables.
|
 |
f(X) is the string representing the function of the x variables. The formulas can contain any number of valid variables.
|
 |
start is a point in n dimension at which the optimization process starts.
|
 |
conjugate gradient settings
 |
gradient method specifies the algorithm used to compute the derivatives. A value of 0 represents the Fletcher Reeves method. A value of 1 represents the Polak Ribiere method. The default is 0.
|
 |
line minimization A value of 0 represents an algorithm without usage of the derivatives. A value of 1 represents an algorithm with usage of the derivatives. The default is 0.
|
|
 |
stopping criteria is the collection of conditions that terminate the optimization. If (function tolerance AND parameter tolerance AND gradient tolerance) OR max iterations OR max function calls then optimization terminates.
 |
function tolerance is the relative change in function value and is defined as abs(current f – prev f)/(abs(curr f)+machine eps). If the relative change in the function value falls below function tolerance, the optimization terminates.
|
 |
parameter tolerance is the relative change in parameter values and is defined as abs(current p – prev p)/(abs(curr p)+machine eps). If the relative change of all the parameter values falls below parameters tolerance, the optimization terminates.
|
 |
gradient tolerance is the 2–norm of the gradient. If the 2–norm of the gradient falls below gradient tolerance, the optimization terminates.
|
 |
max iterations is the largest number of iterations of the major loop of the optimization. If the number of major loop iterations exceeds max iterations, the optimization terminates.
|
 |
max function calls is the largest number of objective function calls allowed before terminating the optimization process.
|
 |
max time (sec) is the maximum amount of time LabVIEW allows between the start and the end of the optimization process. The default is –1. –1 indicates never to time out.
|
|
 |
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
|
 |
minimum is the determined local minimum in n dimension.
|
 |
f(minimum) is the function value of f(X) at the determined minimum.
|
 |
number of function evaluations is the number of times the objective function was called in the optimization process.
|
 |
error out contains error information. This output provides standard error out functionality.
|
Determines a local minimum of a function of n independent variables with the Downhill Simplex method.
 |
function data contains static data that the user-defined function needs at run time.
|
 |
objective function is a reference to the VI that implements the function to optimize. Create this VI by starting from the VI template located at labview\vi.lib\gmath\NumericalOptimization\ucno_objective function template.vit.
 Open template Open template
|
 |
start is a point in n dimension at which the optimization process starts.
|
 |
stopping criteria is the collection of conditions that terminate the optimization. If (function tolerance AND parameter tolerance AND gradient tolerance) OR max iterations OR max function calls then optimization terminates.
 |
function tolerance is the relative change in function value and is defined as abs(current f – prev f)/(abs(curr f)+machine eps). If the relative change in the function value falls below function tolerance, the optimization terminates.
|
 |
parameter tolerance is the relative change in parameter values and is defined as abs(current p – prev p)/(abs(curr p)+machine eps). If the relative change of all the parameter values falls below parameters tolerance, the optimization terminates.
|
 |
gradient tolerance is the 2–norm of the gradient. If the 2–norm of the gradient falls below gradient tolerance, the optimization terminates.
|
 |
max iterations is the largest number of iterations of the major loop of the optimization. If the number of major loop iterations exceeds max iterations, the optimization terminates.
|
 |
max function calls is the largest number of objective function calls allowed before terminating the optimization process.
|
 |
max time (sec) is the maximum amount of time LabVIEW allows between the start and the end of the optimization process. The default is –1. –1 indicates never to time out.
|
|
 |
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
|
 |
minimum is the determined local minimum in n dimension.
|
 |
f(minimum) is the function value of f(X) at the determined minimum.
|
 |
number of function evaluations is the number of times the objective function was called in the optimization process.
|
 |
error out contains error information. This output provides standard error out functionality.
|
 |
X is an array of strings representing the x variables.
|
 |
f(X) is the string representing the function of the x variables. The formulas can contain any number of valid variables.
|
 |
start is a point in n dimension at which the optimization process starts.
|
 |
stopping criteria is the collection of conditions that terminate the optimization. If (function tolerance AND parameter tolerance AND gradient tolerance) OR max iterations OR max function calls then optimization terminates.
 |
function tolerance is the relative change in function value and is defined as abs(current f – prev f)/(abs(curr f)+machine eps). If the relative change in the function value falls below function tolerance, the optimization terminates.
|
 |
parameter tolerance is the relative change in parameter values and is defined as abs(current p – prev p)/(abs(curr p)+machine eps). If the relative change of all the parameter values falls below parameters tolerance, the optimization terminates.
|
 |
gradient tolerance is the 2–norm of the gradient. If the 2–norm of the gradient falls below gradient tolerance, the optimization terminates.
|
 |
max iterations is the largest number of iterations of the major loop of the optimization. If the number of major loop iterations exceeds max iterations, the optimization terminates.
|
 |
max function calls is the largest number of objective function calls allowed before terminating the optimization process.
|
 |
max time (sec) is the maximum amount of time LabVIEW allows between the start and the end of the optimization process. The default is –1. –1 indicates never to time out.
|
|
 |
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
|
 |
minimum is the determined local minimum in n dimension.
|
 |
f(minimum) is the function value of f(X) at the determined minimum.
|
 |
number of function evaluations is the number of times the objective function was called in the optimization process.
|
 |
error out contains error information. This output provides standard error out functionality.
|
For functions that are smooth and have first and second derivatives defined, the Broyden Quasi-Newton algorithm typically converges the fastest. If you experience problems with convergence of the Broyden Quasi-Newton algorithm, the Conjugate Gradient algorithm might be able to solve the problem. The Downhill Simplex algorithm relies only on function evaluations and often is able to find a solution when the function is not smooth and the other algorithms fail to converge.
 Add to the block diagram
Add to the block diagram Find on the palette
Find on the palette