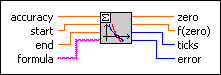
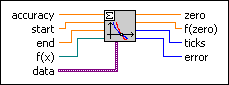
Ridders Zero Finder VI
Owning Palette: Zeros VIs
Requires: Full Development System
Determines a zero of a 1D function in a given interval. The function has to be continuous and has to have different signs at the end points of the interval. You must manually select the polymorphic instance to use.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |