Polynomial Eigenvalues and Vectors VI

Owning Palette: Polynomial VIs

Requires: Full Development System

Solves the polynomial eigenvalue problem. Wire data to the Input Matrices input to determine the polymorphic instance to use or manually select the instance.

Details  

Use the pull-down menu to select an instance of this VI.

Select an instance Polynomial Eigenvalues and Vectors (DBL)Polynomial Eigenvalues and Vectors (CDB)

Add to the block diagram

Find on the palette

Polynomial Eigenvalues and Vectors (DBL)

	Input Matrices is a 3D array of size n*n*p and contains square input matrices of the same size. The input matrices must be square. The matrices are in ascending order of power for Eigenvalues.
	output option determines whether the VI computes Eigenvectors. 0 eigenvalues 1 eigenvalues and vectors (default)
	Eigenvalues is a complex vector of n*p elements and contains all the computed eigenvalues.
	Eigenvectors is an n × (n*p) complex matrix and contains all the computed eigenvectors in its columns.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Polynomial Eigenvalues and Vectors (CDB)

	Input Matrices is a 3D array of size n*n*p and contains square input matrices of the same size. The input matrices must be square. The matrices are in ascending order of power for Eigenvalues.
	output option determines whether the VI computes Eigenvectors. 0 eigenvalues 1 eigenvalues and vectors (default)
	Eigenvalues is a complex vector of n*p elements and contains all the computed eigenvalues.
	Eigenvectors is an n × (n*p) complex matrix and contains all the computed eigenvectors in its columns.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Polynomial Eigenvalues and Vectors Details

The following equation defines the polynomial eigenvalue problem.

where

C₀, C₁, …, C_{p – 1} are square n × n matrices in Input Matrices

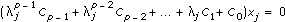
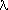_j is the jth element in Eigenvalues

x_j has length n and is the jth column in Eigenvectors with j = 0, 1, …, n*p – 1

If p = 1, the VI calculates eigenvalues and eigenvectors using the following equation.

C₀x_j = _jx_j

If p = 2, the VI calculates generalized eigenvalues and eigenvectors using the following equation.

C₀x_j = –_jC₁x_j