ODE Linear nth Order Symbolic VI
Owning Palette: Ordinary Differential Equations VIs
Requires: Full Development System
Solves an nth-order, homogeneous linear differential equation with constant coefficients in symbolic form.

 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |



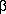 1exp(
1exp(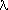 1t) + … +
1t) + … +