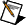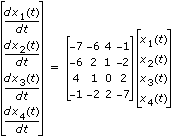Owning Palette: Ordinary Differential Equations VIs
Requires: Full Development System
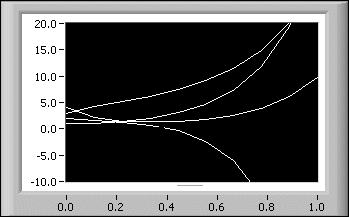
Solves an n-dimension linear system of differential equations with a given start condition. The solution is based on the determination of the eigenvalues and eigenvectors of the underlying matrix. The solution is given in symbolic form.
 Add to the block diagram |
 Find on the palette |
 |
A is the n-by-n matrix describing the linear system. |
|
X0 is the n vector describing the start condition, x[10], …, x[n0]. There is a one-to-one relation between the components of X0 and X. |
 |
formula is a string with the solution of the linear system in the standard formula notation of LabVIEW. The solution vector elements are separated by carriage return. |
 |
error returns any error or warning from the VI. Errors are produced by using the wrong inputs X, X0, and F(X,t). You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
 | Note This VI works properly for almost all cases of real matrices A that can have repeated eigenvalues, complex conjugate eigenvalues, and so on. The exception is the case of a singular eigenvector matrix, that is, a matrix in which the eigenvectors do not span the whole space. An error of –23016 is given if the eigenvector matrix is singular. |
The linear differential equation described by the following system:
with
x1(0) = 1
x2(0) = 2
x3(0) = 3
x4(0) = 4
has the solution
+ 1.62*e(–12.46*t) – 1.28*e(–6.30*t) + 0.63*e(1.34*t) + 0.04*e(5.42*t)
+ 0.84*e(–12.46*t) – 0.29*e(–6.30*t) + 1.51*e(1.34*t) – 0.06*e(5.42*t)
–0.73*e(–12.46*t) + 0.01*e(–6.30*t) + 3.69*e(1.34*t) + 0.02*e(5.42*t)
+ 0.87*e(–12.46*t) + 2.67*e(–6.30*t) + 0.45*e(1.34*t) + 0.01*e(5.42*t)
The following list of parameters shows how to enter the previous equations on the front panel: