Owning Palette: Zeros VIs
Requires: Full Development System
Determines a set of solutions of a nonlinear system of equations in n dimensions beginning with a randomly chosen start point in n dimensions. You must manually select the polymorphic instance to use.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram |
 Find on the palette |
 |
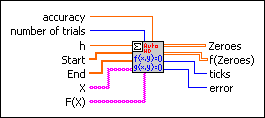
accuracy controls the accuracy of the zero determination. The default is 1.00E-8, which specifies the maximum deviation of the calculated solution from the actual solution. |
 |
number of trials is the elaborate number of randomly chosen start points. The algorithm starts with these points and looks for zeros close to these points. The default is 5. |
|
h is a small distance to calculate derivatives. The default is 1E-8. |
 |
Start is an array describing the left corner of the n-dimension interval. The randomly chosen start points of the zero-finding algorithm can be found in the n-dimensional rectangle spanned by Start and End. |
|
End is an array describing the right corner of the n-dimension interval. The randomly chosen start points of the zero-finding algorithm can be found in the n-dimensional rectangle spanned by Start and End. |
 |
X is an array of strings representing the x variables. If the array of strings contains the variable t, the VI returns an error. |
|
F(X) is an array of strings defining the functions in n dimensions. The formula can contain any number of valid variables. |
 |
Zeros contains the determined zeros of F(X). |
|
F(Zeros) contains the function values of Zeros. Usually, these values are close to 0. |
 |
ticks is the time in milliseconds to analyze the formula and to produce the Zeros. |
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
|
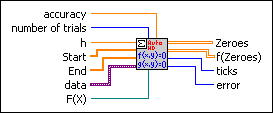
accuracy controls the accuracy of the zero determination. The default is 1.00E-8, which specifies the maximum deviation of the calculated solution from the actual solution. |
|
number of trials is the elaborate number of randomly chosen start points. The algorithm starts with these points and looks for zeros close to these points. The default is 5. |
|
h is a small distance to calculate derivatives. The default is 1E-8. |
|
Start is an array describing the left corner of the n-dimension interval. The randomly chosen start points of the zero-finding algorithm can be found in the n-dimensional rectangle spanned by Start and End. |
|
End is an array describing the right corner of the n-dimension interval. The randomly chosen start points of the zero-finding algorithm can be found in the n-dimensional rectangle spanned by Start and End. |
 |
data contains arbitrary values that pass to the VI that implements the function. |
 |
F(X) is a strictly typed reference to the VI that implements the function. Create this VI by starting from the VI template located in labview\vi.lib\gmath\zero.llb\Zero Finder f(x) nD.vit.
 Open template
|
|
Zeros contains the determined zeros of F(X). |
|
F(Zeros) contains the function values of Zeros. Usually, these values are close to 0. |
|
ticks is the time in milliseconds to analyze the formula and to produce the Zeros. |
|
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
As an example of using the nD Nonlinear System Solver VI, determine the solutions for the following nonlinear system.
2x + 3y + z2 – 6 = 0
–4x + y2 – 4z + 7 = 0
x2 + y + z – 3 = 0
To obtain solutions for the preceding nonlinear system, enter the following values on the front panel.
 | Note You only need to enter the left side of the equations describing the nonlinear system into F(X). The VI assumes that the right side is zero. |
The solutions determined by the VI and returned in Zeros are (1.0000, 1.0000, 1.0000) and (–0.4050, 0.5931, 2.2429).
This algorithm is based on the nD Nonlinear System Single Solution VI.
| Note The algorithm used to find the solution to the nonlinear system is fundamentally stochastic in nature. For example, if number of trials is 3, the VI generates three separate n-dimensional starting points and finds a solution to the system using each of the three starting points. If the nonlinear system has two solutions, the VI might not find both solutions. Generally, the VI finds the solution closest to the starting point for a particular trial. If all three starting points are closest to a particular solution than other solutions, the VI finds the solution closest to the three starting points three times and does not identify other solutions. To improve the chances of finding all solutions, increase number of trials. |
Refer to the Equation Explorer VI in the labview\examples\Mathematics\Scripts and Formulas directory for an example of using the nD Nonlinear System Solver VI.
Open example Find related examples