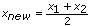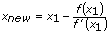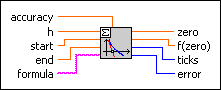
Owning Palette: Zeros VIs
Requires: Full Development System
Determines a zero of a 1D function close to two points with the help of the derivative of this 1D function. The two values form a search limit for the unknown zero of the 1D function. You must manually select the polymorphic instance to use.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram |
 Find on the palette |
 |
accuracy controls the accuracy of the zero determination. The default is 1.00E-8, which specifies the maximum deviation of the calculated solution from the actual solution. |
|
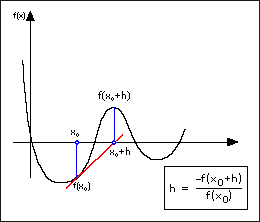
h is the delta value to calculate the derivative of the given formula. The default is 1E-8. |
|
start is the start point of the interval. The default is 0.0. |
|
end is the end point of the interval. The default is 1.0. |
 |
formula is a string representing the function under investigation. The formula can contain any number of valid variables. |
 |
zero is the determined zero of formula. zero is a good approximation only for the exact value. |
|
f(zero) is the function value at the point given by zero. The answer should be very close to zero. |
 |
ticks is the time effort for the whole calculation of the function values in milliseconds. |
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
|
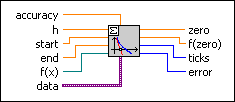
accuracy controls the accuracy of the zero determination. The default is 1.00E-8, which specifies the maximum deviation of the calculated solution from the actual solution. |
|
h is the delta value to calculate the derivative of the given formula. The default is 1E-8. |
|
start is the start point of the interval. The default is 0.0. |
|
end is the end point of the interval. The default is 1.0. |
 |
f(x) is a strictly typed reference to the VI that implements the 1D function. Create this VI by starting from the VI template located in labview\vi.lib\gmath\zero.llb\Zero Finder f(x) 1D.vit.
 Open template
|
 |
data contains arbitrary values that pass to the VI that implements the function. |
|
zero is the determined zero of f(x). zero is a good approximation for only the exact value. |
|
f(zero) is the function value at the point given by zero. The answer should be very close to zero. |
|
ticks is the time effort for the whole calculation of the function values in milliseconds. |
|
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
Let f be the given function. The Newton Raphson Zero Finder VI uses a method that combines the simple midpoint strategy and the Newton strategy.
where x1 and x2 are given guesses with
f(x1) · f(x2) < 0
The following illustration demonstrates the Newton strategy.
