Linear Programming Simplex Method VI
Owning Palette: Optimization VIs
Requires: Full Development System
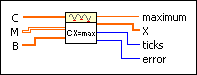
Determines the solution of a linear programming problem.
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
Owning Palette: Optimization VIs
Requires: Full Development System
Determines the solution of a linear programming problem.

 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
 |
C is a vector describing the linear functional to maximize. |
 |
M is a matrix describing the different constraints. |
 |
B is a vector describing the right sides of the constraints inequalities. |
 |
maximum is the maximal value, if it exists, of X under the constraints. |
 |
X is the solution vector. |
 |
ticks is the time in milliseconds for the whole calculation. |
 |
error returns any error or warning condition from the VI. The nonexistence of a solution X leads to an error. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
The following equation defines the optimization problem this VI solves.
cx = max!
with the constraints x  0 and mx
0 and mx  b.
b.
For the optimization problem cx = max!, use the following definitions:
X = (x1, …, xn)
C = (c1, …, cn)
B = (b1, …, bk)
M is a k-by-n matrix.
To solve the optimization problem, you must decide whether an optimal vector X does exist. If the optimal vector does exist, then determine this vector X.
The solution of a linear programming problem is a two-step process. Complete the following steps to solve a linear programming problem.
 | Note The restricted normal formulation seems to be special. But there are many ways to reformulate terms. For example, dx  e is equivalent to –dx e is equivalent to –dx  –e and, dx = e is equivalent to the combination dx –e and, dx = e is equivalent to the combination dx  e and –dx e and –dx  –e. –e. |
Refer to the Geometrical Analysis with Linear Programming VI in the labview\examples\Mathematics\Optimization directory for an example of using the Linear Programming Simplex Method VI.