Lcm VI

Owning Palette: Discrete Math VIs

Requires: Full Development System

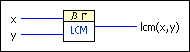
Computes the least common multiple of the input values.

Details  

Add to the block diagram

Find on the palette

	x is an integer.
	y is an integer.
	lcm(x,y) returns the least common multiple of x and y.

Lcm Details

lcm(x,y) is the smallest integer m for which there exist integers c and d such that

x × c = y × d = m

To compute lcm(x,y), consider the prime factorizations of x and y:

x = Π_i p_i^a_i

y = Π_i p_i^b_i

where p_i are all the prime factors of x and y. If p_i does not occur in a factorization, the corresponding exponent is 0. lcm(x,y) then is given by:

lcm(x,y) = Π_i p_i^{max(a_i, b_i)}

For example, the prime factorizations of 12 and 30 are given by:

12 = 2² × 3¹ × 5⁰

30 = 2¹ × 3¹ × 5¹

so

lcm(12,30) = 2² × 3¹ × 5¹ = 60