Kelvin Functions ke VI
Owning Palette: Bessel Functions VIs
Requires: Full Development System
Computes the complex Kelvin function of the second kind.
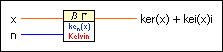
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
Owning Palette: Bessel Functions VIs
Requires: Full Development System
Computes the complex Kelvin function of the second kind.

 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
The complex-valued Kelvin function of the second kind of order v is a solution of the following complex-valued differential equation.
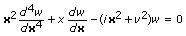
The real and imaginary parts of the Kelvin function of the second kind of order v are solutions of the following differential equation.
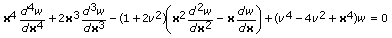
The function is defined according to the following intervals for the input values.
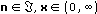
For any integer value of order n, the function is defined for positive real values of x.