Owning Palette: Gamma Functions VIs
Requires: Full Development System
Evaluates the beta function and regularized incomplete beta function. You must manually select the polymorphic instance you want to use.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram |
 Find on the palette |
 |
x is the first argument of the beta function. x must be nonnegative. |
|
y is the second argument of the beta function. y must be nonnegative. |
 |
b(x, y) is the result of the beta function for the given values of x and y. |
|
x is the first argument of the beta function. x must be nonnegative. |
|
y is the second argument of the beta function. y must be nonnegative. |
|
a is the upper limit of the regularized incomplete beta integral and is a real number between 0 and 1. The default value is 1. |
|
b(x, y, a) is the result of the regularized incomplete beta function for the given values of x, y, and a. |
Beta Function
The following equation defines the beta function.
The following intervals for the input values define the function.
Incomplete Beta Function
The following equation defines the regularized incomplete beta function.
The following intervals for the input values define the function.
For any real nonnegative value of upper limit a 
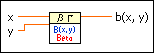
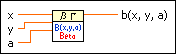
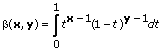
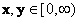
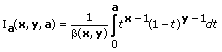
1, the function is defined for all real nonnegative values of x and y.