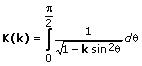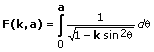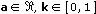Owning Palette: Elliptic Integrals VIs
Requires: Full Development System
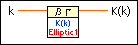
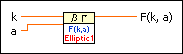
Computes the Legendre elliptic integral of the first kind. You must manually select the polymorphic instance you want to use.
Use the pull-down menu to select an instance of this VI.
 Add to the block diagram |
 Find on the palette |
 |
k is the square of the elliptic modulus. k is a real number between 0 and 1. |
 |
K(k) is the value of the complete elliptic integral of the first kind. |
|
k is the square of the elliptic modulus. k is a real number between 0 and 1. |
|
a is the amplitude of the function, which is the upper limit of the integral. The default value is Pi/2. |
|
F(k, a) is the value of the incomplete elliptic integral of the first kind. |
Complete Elliptic Integral K
The following equation defines the complete elliptic integral of the first kind.
where k is the square of the elliptic modulus.
Incomplete Elliptic Integral F
The following equation defines the incomplete elliptic integral of the first kind.
where k is the square of the elliptic modulus and a is the upper limit, or amplitude, of the integral.
The following intervals for the input values define the function.
LabVIEW supports the entire domain of this function that produces real-valued results. For a real value of upper limit a, the function is defined for all real values of k in the unit interval.