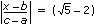Owning Palette: Optimization VIs
Requires: Full Development System
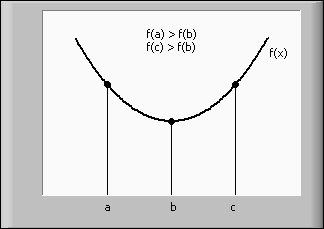
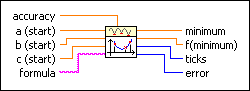
Determines a local minimum of a given 1D function with the help of a bracketing of the minimum. The Golden Section Search method is used.
 Add to the block diagram |
 Find on the palette |
 |
accuracy controls the accuracy of the determined minimum of formula. The method stops if two consecutive approximations differ not more than the value of accuracy. |
|
a is the left point of the bracketing interval. The default is 0.0. |
|
b is the middle point of the bracketing interval. The default is 0.0. |
|
c is the right point of the bracketing interval. The default is 0.0. |
 |
formula is a string describing the function under investigation. The formula can contain any number of valid variables. |
 |
minimum is the determined local minimum of formula. |
|
f(minimum) is the function value at the determined local minimum. |
 |
ticks is the time in milliseconds for the whole calculation. |
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster. |
A bracketing triplet (a, b, c) of a 1D continuous function f is a combination of three points with f(a) > f(b) and f(c) > f(b). This guarantees the existence of a local minimum of f in the interval (a, c).
Beginning with a bracketing triplet (a, b, c), the Golden Section Search method determines a new bracketing triplet with a considerably smaller expansion. Repeating this scheme often yields a good approximation of the local minimum. The following equation essentially calculates the new bracketing point.
(Golden Section Search Method)
The following front panel shows the relationship between a, b, c and f(a), f(b), f(c).
Refer to the Street Illumination Problem VI in the labview\examples\Mathematics\Scripts and Formulas directory for an example of using the Golden Section 1D VI.
Open example Find related examples