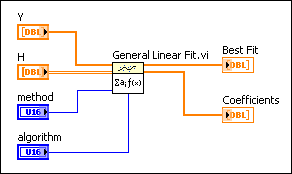
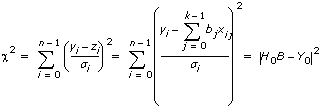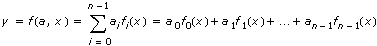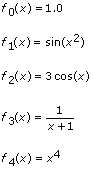|
covariance selector indicates whether the VI computes the covariance matrix.
| 0 | do not compute Covariance | | 1 | compute Covariance |
|
 |
Y is the observed data set Y. The number of elements in Y must equal the number of rows in H.
|
 |
H is the matrix that represents the formula you use to fit the data set (X, Y). Hij are the function values of Xi.
|
 |
Weight is the array of weights for the observations Y. Weight must be the same size as Y. If you do not wire an input to Weight, this VI sets all elements of Weight to 1.
If an element in Weight is less than 0, this VI uses the absolute value of the element.
|
 |
tolerance determines when to stop the iterative adjustment of Coefficients when you use the Least Absolute Residual or Bisquare methods. For the Least Absolute Residual method, if the relative difference of the weighted mean error of the polynomial fit in two successive iterations is less than tolerance, this VI returns the resulting Polynomial Coefficients. For the Bisquare method, if any relative difference between Polynomial Coefficients in two successive iterations is less than tolerance, this VI returns the resulting Polynomial Coefficients.
If tolerance is less than or equal to 0, this VI sets tolerance to 0.0001.
|
 |
method specifies the fitting method.
| 0 | Least Square (default) | | 1 | Least Absolute Residual | | 2 | Bisquare |
|
 |
algorithm specifies the algorithm this VI uses to compute Best Fit. Use the SVD for Rank Deficient H algorithm only if H is rank deficient or does not have a full rank and if all other algorithms are unsuccessful.
| 0 | SVD (default) | | 1 | Givens | | 2 | Givens2 | | 3 | Householder | | 4 | LU Decomposition | | 5 | Cholesky | | 6 | SVD for Rank Deficient H |
|
 |
Best Fit is the fitted data computed by using Coefficients.
|
 |
Coefficients is the set of coefficients that minimize chi squared. The following equation defines 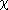 2, where 2, where 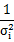 is equal to the i-th element in Weight: is equal to the i-th element in Weight:
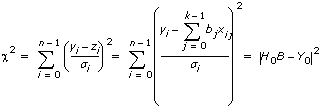
|
 |
Covariance is the matrix of covariance C with k-by-k elements. cjk is the covariance between ai and ak. cjj is the variance of aj. This VI uses the following equation to compute the covariance matrix C:
C = (H0TH0)–1
|
 |
Weight Out returns the actual weight of general linear fitting if method is Bisquare. If method is Least Square or Least Absolute Residual, Weight Out returns the value you enter for Weight.
|
 |
error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.
|
 |
residue returns the weighted mean error of the fitted model. If method is Least Absolute Residual, residue is the weighted mean absolute error. Otherwise, residue is the weighted mean square error.
|
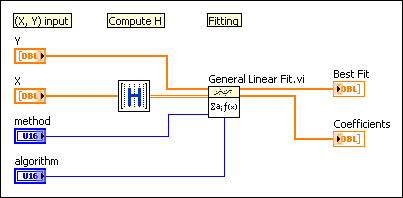
The following linear data model demonstrates how to configure the input parameters and how to use the General Linear Fit VI to obtain the fitted values and the set of least square coefficients a that best represents the relationship of observations (X, Y):
Assume you have a set of observations (X, Y). For example, you can obtain a set of observations through data acquisition. Also, assume you think the relationship between x and y is of the form
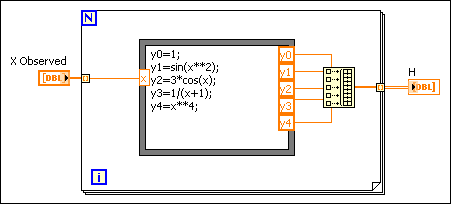
The following block diagram shows the general programming flow for general linear fitting.
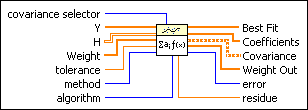
 Add to the block diagram
Add to the block diagram Find on the palette
Find on the palette





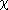 2, where
2, where 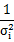 is equal to the i-th element in Weight:
is equal to the i-th element in Weight: