Gcd VI
Owning Palette: Discrete Math VIs
Requires: Full Development System
Computes the greatest common divisor of the input values.
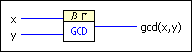
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
Owning Palette: Discrete Math VIs
Requires: Full Development System
Computes the greatest common divisor of the input values.
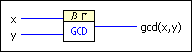
 Add to the block diagram Add to the block diagram |
 Find on the palette Find on the palette |
 |
x is an integer. |
 |
y is an integer. |
 |
gcd(x,y) returns the greatest common divisor of x and y. |
gcd(x,y) is the largest divisor common to x and y.
To compute gcd(x,y), consider the prime factorizations of x and y:
x = Πi piai
y = Πi pibi
where pi are all the prime factors of x and y. If pi does not occur in a factorization, the corresponding exponent is 0. gcd(x,y) then is given by:
gcd(x,y) = Πi pimin(ai , bi)
For example, the prime factorizations of 12 and 30 are given by:
12 = 22 × 31 × 50
30 = 21 × 31 × 51
so
gcd(12, 30) = 21 × 31 × 50 = 6